Pas op: abstraheren is weglaten!

Abstractie is een belangrijk hulpmiddel om problemen aan te pakken. Door alles weg te laten wat er niet toe doet, blijft een veel eenvoudiger model over, waarmee je aan de slag kunt. Als je het goed toepast, komen de fundamentele structuren van een realistische situatie naar boven. Heel nuttig, want er is erg veel in onze wereld dat er niet toe doet als je een specifiek probleem wilt doorgronden.
Er zitten echter ook wat risico’s aan abstraheren. Je moet er natuurlijk wel zeker van zijn dat de zaken die je weg laat, er écht niet toe doen. Ik zal een paar voorbeelden geven waarin dit misgaat of waarin het onhandig is om te veel te schrappen.

Drie schakelaars en één lamp

Puzzeltje: “Stel er is een kamer in een flatgebouw op de derde verdieping met daarin één lamp. De lamp wordt bediend door één van drie schakelaars in de hal op de begane grond. Je moet erachter komen welke van de drie schakelaars dat is, maar je mag maar één keer naar boven lopen om te kijken, wat de lamp doet.” Ik ben verschillende versies tegengekomen van dit raadsel, ook versies met drie lampen in plaats van één. De oplossing komt echter telkens op hetzelfde neer.

Voor velen is het niet zo eenvoudig op te lossen en dat komt meestal doordat ze er niet bij nadenken dat een lamp niet alleen maar ‘aan’ of ‘uit’ staat. Als je beseft dat een lamp behalve licht ook warmte geeft als ie aanstaat, is de oplossing niet meer zo moeilijk te vinden: je zet eerst schakelaar 1 om, wacht een poosje, zet schakelaar 1 uit en zet schakelaar 2 om, en dan loop je naar boven. Als de lamp brandt, is het schakelaar 2. Is de lamp uit, maar nog wel warm, is het schakelaar 1. En in het overblijvende geval (uit én koud) is het schakelaar 3.
De status van de lamp abstraheren tot een simpel ‘aan/uit’ is dus funest voor het vinden van de oplossing. Je kunt echter overdrijven met het in acht nemen van mogelijke andere factoren. Hilarisch is het fictieve interview “What would Feynman do?”.

Recent kwam ik de puzzel tegen op een site waarin het door ene Matthew Silverstone (auteur van het bijzonder vage ‘Blinded by Science’) aangevoerd word als argument om sceptici terecht te wijzen (die zouden namelijk niet verder kijken dan hun neus lang is). Die schrijver begrijpt zelf de puzzel niet helemaal of heeft het slordig van iemand anders overgeschreven. Hij lijkt het met twee keer op en neer lopen te moeten doen! In de vertaling bij Niburu is dat nog duidelijker te zien.
Het te snel verwerpen van mogelijke invloeden en dus met een te simpel model verder redeneren, speelt ook een rol bij de eerste kritiek op Mpemba door zijn leraren en klasgenoten (lees mijn eerdere stuk over het Mpemba-effect: Cool!).

Het gehavende schaakbord

Een andere puzzel waarin te rigoreuze abstractie het je lastig kan maken de oplossing te vinden is ‘the mutilated chessboard’ (bedacht door  Gamow & Stern in 1958). Je begint met een heel schaakbord en 32 dominostenen die ieder precies zo groot zijn als twee velden van het schaakbord. De eerste vraag is of je het schaakbord kunt bedekken met die 32 stenen. Dat is eenvoudig, je legt ze bijvoorbeeld in acht rijen van vier dominostenen zo over het hele bord.
Vervolgens zagen we de linkerbovenhoek en de rechterbenedenhoek van het bord af en vragen of je het overgebleven bord kan bedekken met 31 dominostenen. Dat blijkt na een beetje proberen een stuk lastiger. Sterker nog, snel krijg je het idee dat het helemaal niet kan! Maar bewijs dat dan maar eens. En dan gaat het vaak mis, ook bij slimme wiskundigen.
Ik heb hele mooie bewijzen voorbij zien komen, waarbij het schaakbord wordt voorgesteld als een matrix met 1’en en -1’en, de afgesneden hoekpunten kregen 0 als waarde. De som over de hele matrix is dan 2 (of -2) en er volgt een hele exercitie om aan te tonen dat elke toegelaten betegeling met blokjes van 2×1 die som niet verandert, etc. etc. …

Dat is een wel heel ingewikkelde manier om te zeggen dat een dominosteen telkens één wit en één zwart veld bedekt en dat het gehavende schaakbord meer zwarte dan witte velden heeft overgehouden, omdat we er twee witte velden afgezaagd hebben. Wat je ook probeert, er blijven steeds twee zwarte velden meer onbedekt dan witte.
Op zich doet natuurlijk alleen de vorm van het gehavende schaakbord ertoe, maar wegdenken van de veldkleuring maakt het je lastiger de oplossing te vinden. Overigens lukt het, als je willekeurig twee verschillend gekleurde velden verwijdert, wél altijd (Stelling van Gomory).

Proefpersonen blijken vaker niet zo principiële vegetariërs te zijn!?

Door cijfers alleen als cijfers te bekijken en niet meer te relateren aan waar ze vandaan komen, kun je jezelf ook makkelijk voor de gek houden. Een voorbeeld waarbij ik hier zelf tegen aanliep, is het inmiddels beruchte vleesonderzoek van Stapel, Vonk en Zeelenberg. Toen het persbericht daarover uitkwam, had ik meteen m’n bedenkingen en dat werd sterker toen ik het blog van wetenschapsjournalist Arno van ‘t Hoog las met daarin wat cijfers waarop de uitspraken gebaseerd waren (‘zouden zijn’ moet ik eigenlijk schrijven, maar dit was nog een week voordat de fraude van Stapel naar buiten kwam).
Mijn ‘niet-pluis-gevoel’ werd bevestigd, toen ik van die journalist het pdf-je kreeg met de tabellen van de resultaten van het onderzoek. Eigenlijk wilde ik alleen maar de abstracte percentages terugrekenen naar wat minder abstracte echte getallen om te kijken of het een en ander niet met verkeerde statistische toetsen was berekend.

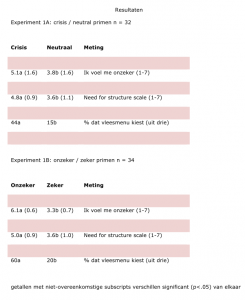
De tabellen waren op zijn minst slordig overgenomen, getallen verkeerd afgerond, ofzo. Mijn rekenkundige bevindingen staan in een later stuk op de website van Arno van ‘t Hoog.

Van Erp: “Er even van uitgaande dat de twee groepen uit 16 personen bestaan leidt 44 procent mooi tot 7,04 dus zullen er 7 van de 16 voor het vleesmenu gekozen hebben. Maar die 15 procent kan ik niet goed terugrekenen 15 procent van 16 =2,4. Als de echte waarde 2 is zou het 13 procent moeten zijn en als het 3 is 19 procent.”
“Vijftien procent kan niet optreden als uitkomst. Oorzaak? Wellicht is de verdeling niet 16-16. Je kunt een iets betere fit krijgen met 18 in de Crisis-groep (8 moeten dan vleesmenu kiezen = 44 procent) en 14 in de neutrale groep (2 het vleesmenu, maar dat zou 14% opleveren). Vreemd dus.”

Ik was overigens niet de enige die dit was opgevallen in de week voor de affaire Stapel losbarstte: Jan van Rongen, die o.a. schrijft op foodlog.nl was de eerste die het openlijk opschreef. Op zijn (latere) weblog is meer te lezen over zijn rekenwerk.

Met betrekking tot het thema abstractie is er echter wel meer op te merken over dit ‘onderzoek’. Ik vond het verbazingwekkend dat er zo makkelijk conclusies werden getrokken uit de keuzes die de proefpersonen gemaakt zouden hebben. De bedoeling was o.a. om twee groepen personen te testen op hun voorkeur voor ‘vlees’ na al dan niet onzeker gemaakt te zijn. Die voorkeur werd getest door ze een keuze te laten maken uit een menu met drie maaltijden, één met vlees, één vegetarisch en één met vis. De proefpersoon moest bedenken dat hij in een restaurant zat en één van drie opties kiezen.

Lijkt nog redelijk, totdat je er wat beter over nadenkt: ik ken geen restaurant met een menu met maar drie keuzes die als plaatje worden aangeboden. Hoe realistisch is ‘t dan te stellen dat je je moet voorstellen dat je op zo’n manier een menukeuze aangeboden krijgt in een restaurant. Is de opzet al niet te abstract gemaakt?
Als je trouwens de opzet en (fictieve) resultaten heel nuchter bekijkt, zou je misschien eerder moeten concluderen dat ‘onzekere gemaakte personen vaker het bovenste plaatje kiezen’. Om uit te sluiten dat het daaraan ligt, hadden ze proefpersonen menu’s moeten aanbieden met de gerechten in verschillende volgordes.
Mijn suggestie aan onderzoekers, die het misschien toch nog eens écht willen uitvoeren, is om met een echt (uitgebreid) menu te werken. De keuzes van proefpersonen  zijn dan wel veel diverser, maar je kunt ze achteraf makkelijk indelen in ‘vlees’ en ‘niet-vlees’.

Pas toen ik heel wat van dit soort observaties opgeschreven had, viel het me op dat een 15% voorkeur voor ‘vlees’ in de neutrale groep eigenlijk volstrekt ongeloofwaardig is. Ook in de tweede test zou het in de neutrale groep maar 20% zijn. Zaten er wellicht buitensporig veel vegetariërs onder de testpersonen? En is het onderzoek dan helemaal niet representatief?
Je moet je bij zulke resultaten afvragen of  de onderzoeksopzet wel echt test wat je beoogd had. Misschien meet je eerder een toenemende tolerantie voor bruine jus als je mensen onzeker maakt. In ieder geval hadden alleen die cijfers al alarmbellen moeten doen afgaan bij Stapels mede-onderzoekers, Vonk en Zeelenberg. Maar dan moet je wel dus wel eerst je abstracte bril afzetten, terugzoeken wat de cijfers ook weer echt zouden moeten aanduiden en je niet blindstaren op het verschil dat mooi aansloot bij de verwachte uitkomst.