Vergezochte wiskunde op Mars

Pak een A4-tje en vouw dat drie keer dubbel. Vouw alles weer open, leg het velletje voor u neer en markeer zes punten zoals op de afbeelding hiernaast. Hang het velletje voor het raam en u bent klaar. U heeft zojuist een boodschap met diepe wiskundige stellingen gecommuniceerd naar uw buren en voorbijgangers: over priemgetallen, Pythagoras, raakpunten van tetraëders met omschreven bollen, en zelfs iets over de spin van elektronen! U gelooft me niet? Komt het over alsof iemand van een andere planeet tegen u zit te kletsen? Mooi zo, dan zit u aardig in de goede richting.

In het Journal of Space Exploration publiceerden de voor mij tot nu toe onbekende heren Horace Crater, Stanley McDaniel en Ananda Sirisena in november vorig jaar een artikel met de titel: The Mounds of Cydonia: Elegant Geology, or Tetrahedral Geometry and Reactions of Pythagoras and Dirac? Al jaren blijken zij bezig met een aantal heuveltjes op Mars die met hun onderlinge posities mogelijk een boodschap van een buitenaardse intelligentie zouden bevatten. De bergjes in kwestie liggen niet ver af van het zogenaamde ‘Marsgezicht’, een bergformatie die op de niet zo scherpe foto’s van de Viking ruimtevaartuigen in 1976 iets weg had van een gezicht. Toen er bij latere missies veel scherpere foto’s beschikbaar kwamen van die regio, bleef er niets over van dat idee.

Wat minder bekend is dat er dus vlakbij dat marsgezicht in de Cydonia regio nog andere formaties liggen die zouden kunnen duiden op kunstmatig constructiewerk. Het gaat dan om een aantal bergjes die op de Vikingfoto’s veel helderder te zien zijn dan andere bergjes. Door allerlei driekhoeken te tekenen met die opvallende punten, viel op dat de hoeken die zo gemaakt worden wel heel erg in de buurt kwamen van rechte hoeken of mooie delen daarvan. Dit was al ontdekt door Richard C. Hoagland, die ook verantwoordelijk was voor de ophef over het ‘Marsgezicht’.

Crater en McDaniel  publiceerden in de loop van de tijd al een aantal artikelen over deze formatie. Zij focussen in eerste instantie op vijf van de twaalf zogenaamde ‘Mounds of Cydonia’ en proberen later een zesde punt in te passen in hun patroon.

Opmerkelijke verhoudingen van de oppervlakten van driehoeken?

Wisknutselen

Het idee achter het zoeken naar wiskundige constructies is dat dat een geschikte manier zou kunnen zijn om met buitenaardsen te communiceren, wiskunde is immers niet erg afhankelijk van taal. Een plaatje van de stelling van Pythagoras zal voor een andere geavanceerde beschaving ook wel herkenbaar zijn. Of de rij priemgetallen zoals in Contact van Carl Sagan.

Wat Crater en consorten allemaal beweren over de vijf (of zes) punten is iets beter te volgen als je een schematische weergave maakt van het geïdealiseerde patroon dat zij menen te zien (de lettertjes r,s en t heb ik er maar even aan toegevoegd):

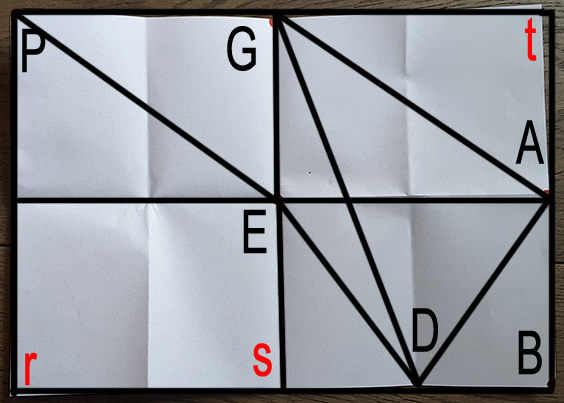
Wat je nu eigenlijk alleen maar moet weten is dat de zijden van de grote rechthoek (PtBr) tot elkaar in de verhouding √2:1 staan. Als je deze rechthoek halveert, kijk bijvoorbeeld naar de rechthoek tBsG, dan heeft ook die weer dezelfde verhouding – en ook weer de rechthoek die daar de helft van is, EABs. Dit is kenmerkend voor de papiermaten die wij kennen als A0, A1, A2, A3, A4, A5, A6 enz. OK, leuk. Maar nu gaan Crater en zijn maten pas echt lekker los.
Eerst even zoeken naar wat priemgetallen. Stellen we de oppervlakte van driekhoek DAB op 1, dan heeft de driehoek EDA oppervlakte 2, de driehoek DAG oppervlakte 3, de vijfhoek BDEGA oppervlakte 5 en het figuur met de hoekpunten BDEPGA oppervlakte 7. Zie hier het begin van de priemgetallenrij 1, 2, 3, 5, 7 aldus de heren. Een wiskundige als ikzelf begint vermoedelijk al met gekromde tenen verder te lezen als iemand stelt dat 1 een priemgetal is, maar het valt natuurlijk ook meteen op dat ze hier wel erg selectief te werk gaan. Waarom niet ook de vierhoek DEGA met oppervlakte 4 meegenomen (die noemen ze overigens wel, ook met oppervlakte, maar nemen ze niet op in het rijtje), of de vijfhoek DEPGA met oppervlakte 6?
De getallen 2,4 en 6 gebruiken de wisknutselaars wel weer om het volgende te beweren:

Then starting with the prime number 3 from the sum 1+2, all of the prime numbers from 5 through 89 can be obtained by adding the three even numbers 2 or 4 or 6 corresponding to the squares of the sides of the middle sized right triangle (which of course satisfy 2+4=6). So, 3+2=5, 5+2=7, 7+4=11, 11+2=13, 13+4=17, 17+2=19, 19+4=23, 23+6=29, 83+6=89.

Bij 89 houdt het op, want het volgende priemgetal, 97, ligt immers 8 verder dan 89. Wat willen de auteurs hier nu mee beweren? Dit kan je immers altijd opschrijven als je ergens de getallen 1 t/m 7 vindt, bijvoorbeeld in Nijntje leert tellen. En waarom 2, 4 en 6? Nou, kijk eerst naar de kleinste rechthoekige driekhoek BDA en stel BD gelijk aan 1. Dan is AB √2 en AD √3  (Pythagoras).  De driehoek AEG heeft dezelfde vorm (‘middle sized right triangle’), maar is een maatje (√2) groter en heeft zijden met lengte √2, √4 en √6, en daar heb je dus die 2,4 en 6. Logisch, toch?

Iets met elektronspin is ook wel terug te vinden in het patroon.

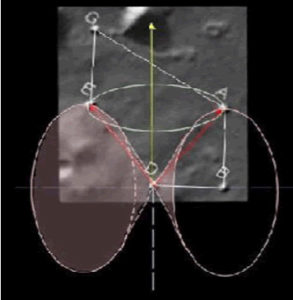
Maar het wordt allemaal nog veel erger. Die √2 die in de verhouding van ons A4-tje naar voren komt, kun je ook wel terugvinden in driedimensionale figuren, bijvoorbeeld een tetraëder. Met een beetje uitproberen kun je een gedeelte van het patroon dan weer terugvinden in een doorsnijding daarvan, of de voorkomende hoeken in de ‘breedtegraad’ waarop de basis van de tetraëder ligt in de omschreven bol. Tsja. Je zou nu even goed kunnen nadenken over wat dat kan betekenen, maar de auteurs schotelen je alweer een ander mirakel voor: met die √2 lukt het je ook om een projectie van elektronenspin precies op het plaatje af te beelden! Ik zal u de details maar besparen.
Ik snap overigens wel waarom de auteurs die tetraëder er met de haren bijslepen. De Platonische lichamen, waartoe de tetraëder behoort, zijn net als de priemgetallen wel geopperd als duidelijk herkenbaar wiskundig materiaal, dat geschikt zou zijn om een betekenisvol signaal richting aliens te sturen. Maar dat is volgens mij toch wel iets anders dan ergens een √2 in verstoppen.

Hoe creëer je zoiets?

Op basis van de hoge resolutie beelden wist een bevriende geoloog de auteurs te vertellen dat de heuvels waarschijnlijk de restanten van moddervulkanen zijn. Die hebben dan wel een natuurlijke oorsprong, maar, zo redeneren de auteurs, als wij op aarde al per ongeluk een moddereruptie kunnen veroorzaken, dan zouden hoogontwikkelde aliens dat vast wel met voorbedachte rade en op een gekozen locatie kunnen doen. Ze wijzen dan op de ramp in Sidoarjo, Indonesië, waar uit een boorgat al sinds 2006 een enorme hoeveelheid modder stroomt. En ja, als er al een aantal heuvels op de goeie plek zitten, hoef je het patroon misschien alleen maar aan te vullen met een paar kunstmatig veroorzaakte vulkanen. Is dan wel weer mazzel dat er later niet nieuwe heuvels zijn onstaan op de plek waar je je patroon aan het creëren was. Die zouden het hele schema in het honderd hebben doen lopen …

Hoe precies is het patroon?

Uiteindelijk draait het toch om die vraag. Op de foto’s van de Vikings had de kleinst waarneembare structuur een afmeting van ongeveer honderd meter, maar het nieuwere beeldmateriaal heeft een veel groter oplossend vermogen (5 m per pixel). Het is misschien slim om zelf eens te kijken op dat beeldmateriaal dat beschikbaar is gekomen. Hieronder de foto van de regio genomen door de Mars Orbiter in 2014 (klik voor een uitvergroting):

De 6 punten waarop het artikel gebaseerd is tov het “Marsgezicht” [foto: MRO HiRISE CTX D21_035487_2215_XN_41N009W]

Wat levert het nieuwe beeldmateriaal nu op voor de precisie van het patroon? Want dat is naast het geologische verhaal eigenlijk het enige echt nieuwe aan dit artikel, al dat geneuzel met priemgetallen en elektronenspin stond al in een artikel van Crater uit 2007. De auteurs geven voor allerlei hoeken van de driehoeken wat de ideale grootte zou zijn en wat die is als je gaat meten aan de foto’s na die eerst zo gedraaid te hebben dat je van ‘bovenaf’ tegen de formatie aankijkt). De afwijkingen lopen uiteen van een paar tienden tot enkele graden. Wat dat op de grond betekent voor de afwijkingen van de toppen van de heuvels ten opzichte van de ideale punten vertellen de auteurs niet.
In de berekeningen gebruiken de de auteurs overigens niet de toppen van de heuveltjes als vaste punten van het patroon, maar laten ze nog enige bewegingsvrijheid toe voor die punten. Een computerprogramma berekende namelijk de beste fit als je de punten mag laten schuiven over een rechthoekje dat je om het bergje trekt. Ik leid daaruit af dat de hoekpunten op enkele tientallen meters van de top van een bergje kunnen liggen. Die fysieke toppen zijn natuurlijk ook maar een suggestie voor de punten van het patroon, moeten we maar denken. Maar als ik kijk naar de mate van nauwkeurigheid per fotoset, valt mij op dat de afwijkingen ten opzichte van het ideale met name bij de nieuwste een stuk forser zijn geworden, dat lijkt niet echt goed nieuws voor de speculatieve hypothese.

De auteurs beweren desalniettemin dat de kans dat je zo’n patroon aantreft bij toeval astronomisch klein is. De wiskundige Ralph Greenberg bekritiseerde dit al eerder door er op te wijzen dat Crater c.s. alleen kijken naar de hoeken uit hun favoriete patroon. Als je naar alle mogelijke wiskundig interessante patronen kijkt, zal je waarschijnlijk zien dat er veel vaker zo’n interessant verhaaltje is op te hangen als je willekeurig twaalf punten op een vlak tekent (en met de gehanteerde methode om een patroon te fitten). Met de gegeven vijf punten ligt het misschien voor de hand de gevonden waarde √2 tot een belangrijke boodschap te verheffen, maar hadden de punten iets anders gelegen, dan hadden Crater en co wellicht een soortgelijk verhaal kunnen houden met de Gulden Snede, π of e. Mij valt ook op dat de auteurs geen moeite gedaan hebben om te kijken of de twaalf opvallende punten van de Vikingopnames in het nieuwe beeldmateriaal er ook nog zo duidelijk uitspringen. Heuvel B lijkt mij bijvoorbeeld al helemaal niet meer zo opvallend.

Het heeft natuurlijk allemaal veel weg van het rekenen aan de piramides of aan de fiets van professor De Jager.