De afgelopen tijd heb ik het veel gehad over de ideeën van de organisator van de platte aarde-conferentie op 28 en 29 september. Dat doe ik ter voorbereiding voor de onwaarschijnlijke zaken die tijdens het congres langs zullen komen. Dit artikel gaat over overeenkomsten tussen skeptici en platte-aardegelovigen en eigen waarnemingen die men kan doen aangaande de vorm van de aarde.
Heslinga heeft bij zijn geloof in de platte aarde en de maanlandingen, die laatste zouden niet hebben plaatsgevonden, complotten nodig. Skeptici, die het tot hun opdracht maken om buitengewone en pseudowetenschappelijke beweringen te onderzoeken, verschillen hier meestal in doordat ze geen of te zwak bewijs vinden voor deze complotten. Ook in hun waarheidscriterium verschillen Heslinga en andere platte-aardegelovigen met skeptici. Waar skeptici vooral uitgaan van bewijzen die controleerbaar en reproduceerbaar zijn, zoals in de wetenschap, houden Heslinga en medestanders het op hun gevoel en eigen gezond verstand. Eén vraag die hierbij opkomt is of deze groepen überhaupt nog met elkaar in contact kunnen treden, als ze zouden willen.

Overeenkomst skeptici en platte-aardegelovigen?
Mick West geeft in zijn boek Escaping the rabbit hole aan dat een aspect van het contact ligt in het vinden van een gemeenschappelijke grond (p.148). In Skepsis podcast #6 spreekt Pepijn van Erp over zo’n gemeenschappelijke grond tussen sommige platte-aardegelovigen en skeptici. Namelijk dat bij beiden de instelling aanwezig is om hun ideeën te toetsen en niet zomaar iets aan te nemen van foto’s of wat in de boekjes staat. Ook Heslinga deelt deze instelling onder andere in wat hij zegt over platte-aardegelovigen: “Flat earthers zijn meestal individuen die zelf op onderzoek uit gaan” en dat complotdenkers enkel vragen zetten bij wat ze aangeleerd krijgen en zelf onderzoek daarnaar doen. Ook gaan zijn observaties over de kromming van de aarde over “waarnemen”(Harambam, p.249-250) en spreekt hij in zijn presentatie “de aardse waarheid” in Heel van 2022 over een laserexperiment op het IJsselmeer tussen Enkhuizen en Lelystad. Kortom, sommige skeptici en platte-aardegelovigen kunnen elkaar vinden in het uitvoeren van eigen onderzoek.
Het moge duidelijk zijn dat niet iedere, of zelfs de meeste, platte-aardegelovigen het eigen onderzoek vooropstelt en dat meer als een excuus gebruiken om geloofwaardiger over te komen (Verhoft, p.96).
Om met deze overeenkomst verder te gaan heb ik wat simpel eigen onderzoek verricht en waarnemingen gedaan om erachter te komen wat de vorm van de aarde is. Hieronder enkele van mijn bevindingen.
Kromming van de aarde
Heslinga vraagt zich af waar de kromming van de aarde te bekennen is. Zoals hij zelf aangeeft: als er een kromming is, dan zouden objecten op een gegeven moment achter de horizon verdwijnen. Zelf denkt hij dat dit “(bij benadering) 8 inches, vermenigvuldigd met het kwadraat van de afstand in mijlen” is (Harambam, p.249). Hierdoor zouden objecten al snel verborgen zijn achter de kromming. Deze formule houdt echter geen rekening met de hoogte van de waarnemer en de weersomstandigheden, die laatste kunnen invloed hebben op fenomenen als refractie. Door deze variabelen kun je al snel meer zien dan Heslinga verwacht. Zo zou bij een waarnemershoogte van 1,6 meter een object bij een afstand van 10 kilometer niet 7,85 meter verdwenen zijn, maar 2,36 meter (refractie niet meegenomen).
Als de aarde plat was zou je volgens Heslinga alles wat onder de horizonlijn ligt richting de horizon zien stijgen totdat je het niet meer ziet. En alles boven de horizonlijn richting de horizon zien dalen totdat je het niet meer ziet. De horizonlijn rijst volgens Heslinga ook altijd naar ooghoogte.
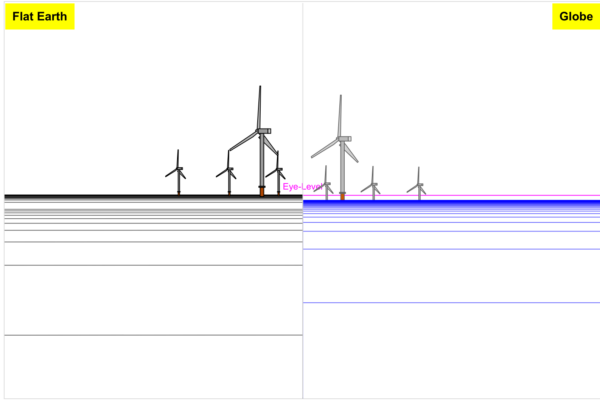
Gewapend met deze informatie ben ik naar het strand gegaan om waarnemingen van windmolens op zee te maken en te zien met welke voorspellingen van de bolvormige – of platte aarde deze waarnemingen het meest overeenkwamen.
Hierboven een weergave van wat beide modellen voorspellen wat een waarnemer op 1,6 meter ooghoogte met een verrekijker zou moeten kunnen zien van windmolens op 13 en 24 km afstand. Links zien we de verwachting van de platte aarde waarbij de windmolens op 24 km afstand ongeveer de helft kleiner lijken en dichter bij de horizon lijken te staan maar nog steeds in hun geheel te zien zouden zijn.
Rechts het beeld van een bolvormige aarde met een kromming waardoor de onderkant van de windmolens op 24 km afstand duidelijk achter de horizon verdwijnt. Hieronder een foto om een beeld te geven van mijn waarneming. De foto’s in dit artikel zijn niet mijn bewijzen, de bewijzen zijn mijn waarnemingen, de foto’s zijn illustraties van hetgeen ik ongeveer waarnam. Mijn waarnemingen komen het meest overeen met wat je op een bolvormige aarde zou verwachten. Namelijk het ontbreken van het onderste gedeelte van de verste windmolens.


We kunnen nog meer zien aan de windmolens door de hoogte van de waarnemer te veranderen. Op een platte aarde zou de hoogte niet veel uitmaken, maar op een bolvormige aarde kun je voorbij de horizon kijken die je ziet vanaf een lager standpunt, je kunt meer zien achter de kromming (Verhoft, p.114). En dit nam ik ook waar toen ik op ongeveer 11 meter en 25 meter hoogte stond. Hoe hoger de waarneming gedaan wordt, hoe meer er te zien is van de windmolens. Maar de horizon leek niet met mijn ooghoogte mee te stijgen wat volgens Heslinga wel zou moeten gebeuren. Het zou dan lijken alsof er achter de achterste windmolens water zou liggen boven hun paal. Maar dit is dus niet waargenomen.
Bezwaren van Heslinga
Met een verrekijker was de onderkant van de windmolen niet terug te halen. Die bleef verborgen. Pas toen ik hogerop klom werd de onderkant van de windmolens meer zichtbaar. Hiermee vervalt één van de voorspellingen van Heslinga. Namelijk, dat je met een verrekijker de onderkant van objecten terug kunt halen. Een andere hypothese voor mijn waarnemingen op een platte aarde is dat het om een luchtspiegeling zou gaan. Mocht dit echter het geval zijn zou je niet alleen vertekeningen verwachten bij de windmolens, maar ook de horizon. Dit is ook niet waargenomen.

Als laatst heeft Heslinga het over perspectief. Heslinga’s presentatie in Heel laat het bovenstaande beeld zien op 36:15 van deel 2. Hierin zou het verdwijnen van de zon geïllustreerd worden aan de hand van een tafel en een muntje. Dit zou verklaren waarom de onderkant verdwijnt terwijl je het bij inzoomen terughaalt. Wat opvalt is dat de camera schuin omhoog ten opzichte van de tafelrand lijkt te staan. Hierdoor is het onderste gedeelte al verscholen achter de tafel. De camera staat dus niet op gelijke hoogte met de tafelrand maar iets eronder. Bij het reproduceren van dit experiment behaalde ik ook alleen maar dezelfde resultaten als de camera zich onder de tafelrand bevond. Dat het inzoomen van de camera kan zorgen dat het object teruggehaald wordt ligt aan het feit dat bij het inzoomen de intreepupil van de camera wordt vergroot waardoor er meer licht van boven de tafelrand wordt opgevangen. Dit is niet de situatie als je op de aarde staat, tenzij je je in een kuil bevindt. Hierdoor is de gemaakte waarneming ook niet te verklaren door een vreemd soort perspectief van een platte aarde. Dus blijft de bolvormige aarde de beste verklaring voor de gemaakte waarnemingen.
Andere observaties
Wie zich voor deze waarneming toch al op het strand begeeft, kan ook wachten op de zonsondergang. Die zoals we hierboven behandeld hebben van onderaf verdwijnt. Dit wordt veroorzaakt door de draaiing van de aarde, waardoor dat gedeelte van de aarde zich wegdraait van het zonlicht. Let ook op wolken en vliegtuigen na de zonsondergang. Deze kunnen nog verlicht worden door de zonnestralen vanonder de horizon. Deze waarnemingen zijn moeilijk te verklaren in Heslinga’s platte-aardemodel, omdat de zon niet ondergaat maar rondjes draait en zich veelal boven deze wolken of vliegtuigen bevindt. Niet hoger dan 15 km hoogte volgens Heslinga’s lezing in Heel deel 2 op tijdstip 31 min 10 sec. Dat deze hoogte meerdere problemen met zich meebrengt zullen we maar even terzijde laten.

Zo zien we dat een dagje strand een perfecte mogelijkheid is voor platte-aardegelovigen en skeptici om waarnemingen te doen van de kromming van de aarde. Windmolens en de ondergaande zon als voornaamste waarnemingsobjecten. Al dan niet afgewisseld met een experimentje van een tafel en een muntje. Ik denk dat zo’n dagje een betere activiteit is dan de conferentie.
Literatuur:
Harambam, J. Kuiper, M. Vaessen, R. The Truth Is Out There. Volt. 2021.
Verhoft, F. De platte aarde: een rondleiding. Uitgeverij ASP nv. 2020. – bespreking uit Skepter
West, M. Escaping the rabbit hole revised & updated. Skyhorse Publishing. 2023. Ebook. – bespreking uit Skepter
Presentaties:
De Aardse Waarheid, Heel deel 1. Frans Heslinga. 2022.
De Aardse Waarheid, Heel deel 2. Frans Heslinga. 2022.
Documentaire: Flat or Curved: The world of Flat Earth. 2020.

Dat de horizon op ooghoogte zou zijn is een van de leugens van de platte-aarde-sekte. Even rekenen leert dat de zgn diphoek (hoeveel graden de horizon onder de horizontaal ligt) heel erg klein is. Pas vanuit een vliegtuig op ca 10 km hoogte is dit een paar graden. Onmogelijk te registreren zonder een referentie lijn. Met een beetje “do your own research” kun je de diphoek zichtbaar maken. Bijv een flesjeswaterpas meefotograferen, of een theodolietapp op je smartphone,zoals dioptra. Kort geleden heb ik daarmee de diphoek vanuit een lijnvliegtuig meerdere keren gefotografeerd. De horizon is nooit op oogniveau.
Interessant dat Heslinga beweert dat de zon op ca 15 km hoogte is. De meeste flerfs vermijden angstvallig een hoogte te specificeren. En begrijpelijk. Want hoe wil je dit rijmen met de hoekhoogte van de zon boven de horizon om 12 u zonnetijd tijdens de equinox; deze is voor iedere breedtegraad (B) gelijk aan 90°– B; tegelijkertijd is overal op aarde de afstand tussen twee opeenvolgende breedtegraadwaardes (51>52 of 12>13 etc.) dezelfde 111 km. Onmogelijk op een platte Aarde, je krijgt voor iedere breedtegraad een andere zonshoogte.
De muntje tafel goocheltruc is zeer grondig ontmaskerd door dave mckeegan (professionele fotograaf) in dit filmpje
https://youtu.be/1cZgGOPUEDs?si=YwBYFi583D6LN-YB
En als je nog wat langer wacht totdat je de sterrenhemel kunt zien, zijn er nog allerlei andere observaties die de platte aarde ontkrachten.
Zo zie je hier dat alle sterren tegen de klok in rond de (noord)poolster roteren. Kijk je echter vanuit bijvoorbeeld Zuid-Afrika naar deze rotatie, dan draaien ze juist de andere kant op. En oh, je ziet daar ook compleet andere constellaties dan hier.
Rara hoe kan dat, wanneer we allemaal op een platte schijf staan en dus allemaal ongeveer dezelfde sterrenhemel zouden moeten zien, met dezelfde bewegingsrichtingen?
En zo zijn er nog talloze andere dingen te verzinnen met bijvoorbeeld de maan — hoe hoog hangt ‘ie? Wanneer dit slechts tientallen of desnoods honderden kilometers zijn, waarom ziet iedereen ter wereld ‘m even groot?
Tja, waar zitten dan zon en maan aan vast?
Die zitten natuurlijk allemaal aan de koepel, die de platte aarde omsluit, of ze worden er op geprojecteerd.
@Renate1
Ik ben natuurlijk een domme lastpost, maar wie bedient de projector? En hoeft daar nooit een nieuw lampje in?
@ Hans
Dat zullen de Illuminati wel zijn. Die zitten immers overal achter volgens deze warhoofden?
Jaa, dat zullen “ze” ons natuurlijk nooit vertellen!
En wanneer je er wat simpele goniometrie bij haalt, kun je al heel snel onomstotelijk aantonen dat de afstand tussen de aarde en de zon (of maan) vele malen groter is dan welke afstand op aarde ook. En dan zit je dus als platzo met het probleem dat de hele schijf is verlicht of niet, in plaats van de helft verlicht en de andere helft donker.
Enzovoort enzovoort enzovoort.
Het echte probleem is natuurlijk dat Ware Gelovigen zich nooit zullen laten overtuigen door zelfs de beste, meest mathematisch waterdichte argumenten. Ze zullen nooit toegeven dat ze ernaast zitten, zelfs al moeten ze zich daarvoor in de meest idiote bochten wringen en met de meest absurde of vergezochte (en doorgaans foute) ‘verklaringen’ komen.
Zo had ik laatst dus een discussie met een homeopathiegelovige op de retraction page van een homeopathie-artikel. De persoon in kwestie weigerde mordicus toe te geven dat het verdunnen van van een stof met 1:10^60 en het vervolgens bij analyse aantreffen van significante hoeveelheden van exact diezelfde stof een absolute, onverenigbare tegenspraak opleverde, ongeacht op welke manier ik hem de materie uitlegde, en ook ongeacht het feit dat dit de hoofdreden van terugtrekking van het artikel was (een reden die hij dan ook weigerde te erkennen).
@Richard Rasker
Goniometrie is natuurlijk een specifiek wiskundegebied dat erg veel mensen boven de pet gaat. En dan kan het vanzelfsprekend en dientengevolge niet waar zijn dat de compotters het bij het verkeerde eind hebben. Die gebruiken nl. hun “gezond verstand”. 1:10^60 is al helemaal onvoorstelbaar, vandaar de nog steeds talloze mensen die zeggen te “geloven in homeopathie” (“Dat is toch iets met planten en ben jij dan tegen genezen met planten?”). Hun auto rijdt vast niet op benzine D60…
Kortgeleden heb ik nog iemand geprobeerd uit te leggen wat een logaritmische schaal inhoudt. Glazige ogen als resultaat. Zulke mensen kun je álles wijsmaken.
Als je googelt wat Heslinga allemaal aan onzinnigs beweert, kun je je afvragen wat de man nog buiten een gesticht houdt; ik denk dat de oplossing daar ligt dat de overgrote meerderheid aan volgers zijn onzin niet kan overzien.
Maar ja, wat wil je, als mensen bijna trots lijken de zijn dat ze niets van wiskunde snappen. Want wat heb je nu in het dagelijks leven aan wis- natuur- en scheikunde, als je er je brood niet mee verdient? Om dingen uit te rekenen heb je een rekenmachine, dus dat is allemaal overbodige nonsens.
Nou ja, misschien is enige kennis van exacte vakken toch wel nuttig om door de kletsverhaaltjes van onzinverkondigers te prikken. En bij een rekenmachine kan je wel eens een knopje te veel of te weinig indrukken en dan is het op z’n minst handig als je enig idee hebt wat de juiste uitkomst zou moeten zijn. Ik kan me nog herinneren dat iemand bij AH voor een halve fles champagne minder dan de helft van de prijs van een hele fles champagne van hetzelfde merk rekende. (Tel uit je winst.)