Over bijna-doodervaringen is al heel wat afgesteggeld tussen skeptici en gelovigen. De laatste jaren ging het vooral over de ideeën van Pim van Lommel, die stelt dat de bijna-doodervaringen duiden op een leven na de dood, een voorbestaan als non-lokaal, niet lichaamsgebonden bewustzijn. Of zoiets. Geesteswetenschapper Maureen Venselaar schreef in 2011 een boek dat weer een heel andere visie op het fenomeen geeft, volgens haar zonder een beroep te doen op dit soort bovennatuurlijke zaken: De (bijna-)dood ontrafeld – in het licht van de Fibonacci-code.
Het boek biedt: “een compleet nieuwe visie op de (bijna-)doodervaring op basis van de vijf-fasen-theorie© en de menselijke en universele natuur, via (astro)fysica. Het beschrijft álle kenmerken (in tegenstelling tot de neurologische en bovennatuurlijke verklaring) en bevat tevens 10 nieuwe kenmerken© en tal van bijzondere overeenkomsten met wereldbeschouwingen. De nieuwe theorie kan bevestigd worden door honderden bijna-doodervaringen.” Tsjongejongejonge.
Venselaar schrijft op haar website dat ze op haar theorie had willen promoveren, maar dat vijf aangeschreven universiteiten geen mogelijkheid tot begeleiding van deze interdisciplinaire studie zagen en dat het mede daardoor niet doorging. Wie echter even op haar website rondneust, zal het vermoeden krijgen dat die universiteiten snel doorhadden wat voor onzin Venselaar zoal vertelt en het eerste het beste formele smoesje hebben gebruikt om haar vriendelijk af te poeieren.
Misschien is het aardig om te kijken wat anderen van haar theorie vinden, zoals Titus Rivas, die actief is bij het Netwerk Nabij-de-Doodervaring (voorheen Stichting Merkawah). Rivas schrijft:
De auteur kan in ieder geval aardig schrijven en geeft blijk van een zeer grondige literatuurstudie. Bovendien legt zij hoe dan ook een grote vindingrijkheid en originaliteit aan de dag. Zo meent ze in alle ernst dat we pas een fijnstoffelijk “astraal” lichaam krijgen tijdens een hartstilstand en dat de vorm hiervan samenhangt met de hoeveelheid vrijkomende fotonen (sic). Volgens mij is er geen overtuigend bewijsmateriaal voor deze voorstelling van zaken, maar de gedachte is zeker origineel. Tot mijn verbazing blijkt ook de verwijzing naar de zogeheten Fibonacci-code niet slechts nageprate onzin, omdat er BDE’s zijn waarin een trechtervormig verschijnsel wordt genoemd dat hiermee (enigszins) lijkt samen te hangen.
en:
De auteur hanteert het bekende hermetische correspondentie-principe uit de esoterische traditie dat men voor elk fenomeen in de mens (microkosmos) een parallel zou kunnen vinden in het universum (macrokosmos). Dit principe heeft echter geen rationele fundering en stamt in feite uit een tijdperk waarin men de mens als middelpunt van de schepping beschouwde. Het is daarom nogal gewaagd om er in 2011 nog zomaar van uit te gaan. Helaas is het grootste deel van het boek op deze dubieuze denktrant gestoeld. Allerlei conclusies berusten niet op rationele gevolgtrekkingen maar op veronderstelde, zuiver speculatieve analogieën die alleen van belang zijn als men gelooft in een feilloze hermetische correspondentie. Een absurde consequentie hiervan is dat Venselaar praktisch in alle gevallen de voorkeur geeft aan een letterlijke interpretatie van aspecten van BDE’s en symbolische interpretaties systematisch negeert.
Nu is Rivas geen onbekende van Skepsis (met Rob Nanninga lag hij bijvoorbeeld in de clinch over diens bespreking van Rivas’ boek waarin hij herinneringen aan ‘vorige levens’ als bewijs voor reïncarnatie opvoert), maar hier zegt hij wel wat zinnige dingen. Rivas gaat in zijn recensie echter nauwelijks in op haar pseudowetenschappelijke teksten met natuurkundig termen als:
Belangrijk is te weten dat atomen in ons lichaam instabiel kunnen raken, want door diezelfde instabiliteit komen er namelijk fotonen vrij (fotonen=lichtenergie). Juist dit verschijnsel van vrijkomen van zo’n soort licht/fotonen leidt waarschijnlijk tot de vorming van ons astrale (ziels)lichaam, bij onze (bijna)dood. Ons fysieke lichaam zal bij onze (bijna)dood op (sub)atomair niveau instabiel worden. Dit zal aanvoelen als kleine explosies en trillingen…. Het ziet ernaar uit dat deze diep fysische verschijnselen gekoppeld kunnen worden aan de wetenschappelijke onderzoeksresultaten van prof. A. Gurwitsch en prof. F-A. Popp.
Voor de ideeën over biofotonen van Fritz-Albrecht Popp verwijs ik de lezer naar wat Marcel Hulspas en Jan Willem Nienhuys daarover in Tussen Waarheid en Waanzin: een encyclopedie der pseudo-wetenschappen schreven (Venselaar noemde Popp op haar website eerst nog als Nobelprijswinnaar, maar dat heeft ze inmiddels bijna overal gewijzigd). De samenvatting van haar boek geeft de indruk dat ze echt van alles en nog wat aan elkaar plakt: zwart gaten (groot en klein), wormgaten, torussen en vortices, snaartheorie, dopplereffect, magnetisme.
Maar hoe past de Fibonacci-reeks in dit verhaal? Iets met die trechtervorm als we op Rivas zijn bespreking mogen afgaan. De stukjes tekst uit het boek, die op haar website staan, geven hier nauwelijks een aanknopingspunt voor. En een boek met zoveel nonsens aanschaffen voor het bevredigen van een nieuwsgierig vraagje, gaat mij ook wat ver. Er staat echter een lezing van haar online. Die hield ze in 2014, waar anders dan bij het Studium Generale van de TU Delft onder leiding van Coen Vermeeren. Redelijk aan het einde van haar presentatie, dat bestaat uit het opmerken van ogenschijnlijk volstrekt willekeurig verbanden, komt de Fibonacci-reeks aan de orde.
Die Fibonacci-spiraal is gebaseerd op de bekende Fibonacci-reeks. Dat is een getallenrij die begint met twee énen en je vindt de volgende getallen in de rij door telkens de twee voorgaande op te tellen: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, enz. Hoe je verder in de rij kijkt, hoe beter de verhouding van twee opeenvolgende getallen de Gulden Snede benadert. Die verhouding wordt aangeduid met de Griekse letter φ en is ongeveer 1,618. Die Fibonaccigetallen kom je nogal eens tegen in de natuur en het veel mensen denken dat je de Gulden Snede ook tegenkomt in oude bouwwerken en schilderijen, maar dat is grotendeels onzin (zie Tien mythes over de Gulden Snede).
Je kunt er een grappige kromme mee maken door vierkantjes aan elkaar te plakken met zijdes die oplopen met de getallen in de reeks en er vervolgens kwart cirkels in te tekenen:
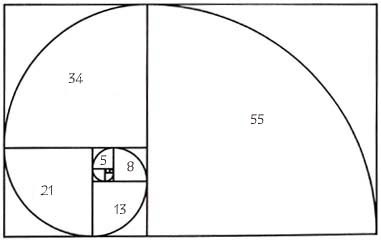
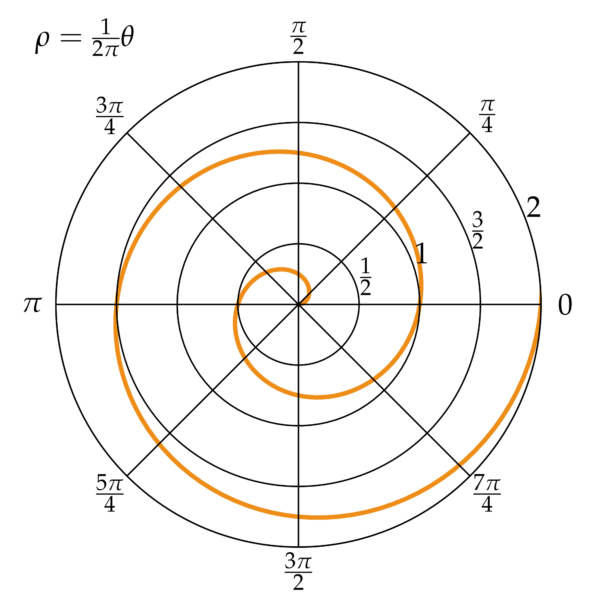
Venselaar suggereert dat hier een driedimensionale spiraal van kunt maken die in een kegel past door de oorsprong van de spiraal als het ware omhoog te trekken uit het vlak. Dat mag ze toch een keer wiskundig laten zien, want dat werkt niet echt. De Fibonacci-spiraal is namelijk helemaal niet zo’n nette curve, omdat het aan elkaar geplakte cirkelboogjes met verschillende straal zijn. Er is wel een logaritmische spiraal met groeifactor φ, waarvoor de Fibonacci-spiraal een aardige benadering is, maar ook die past niet op de kegel op een manier die lijkt op de titelafbeelding van haar boek, waarbij het beeld van een trechter naar voren treedt. Je kunt natuurlijk elke afbeelding in het platte vlak wel projecteren op een kegel, maar in met deze spiralen gaat het er echt anders uitzien dan zo’n trechter met windingen die op regelmatige afstand van elkaar staan.
Een spiraal waarmee je wel kunt doen wat Venselaar wil, is de Archimedische spiraal, maar daar hangen verder niet zoveel zweverige praatjes omheen te vertellen – elk voordeel heb z’n nadeel.
Toch is het best knap om meteen met de subtitel en de cover van je boek de wiskunde geweld aan te doen. Maar ach, eigenlijk was toch ook weer geen kegel, want even verderop (1:26:00) in haar presentatie blijkt die zandloper (2 kegels op elkaar) het ‘klokhuis’ van een torus te zijn:
O, tuurlijk: een stabiele vorm met ‘stromen naar binnen en naar buiten’ die ook nog onderdeel zijn van de chaostheorie … Misschien moet je eerst een heel stel bijna-doodervaringen hebben meegemaakt om dit allemaal nog te vatten.

