Voor het grote publiek zal Klaas van Egmond vooral bekend staan als iemand die een voortrekkersrol speelt in het duurzaamheidsdebat. Hier op Kloptdatwel kennen we ook zijn interesses in zweverige zaken als graancirkels, pseudogeschiedenis en mediums. Toevallig stuitte ik op dit interview met hem en ik denk dat we weer een nieuw hoofdstukje kunnen toevoegen aan de merkwaardige hobby’s van Van Egmond. Kijk eerst zelf, daarna zal ik er commentaar op geven.
https://www.youtube.com/watch?v=-zyGfwsadK8
NB ik had bij het publiceren van deze post per ongeluk het kortere inleidende interview over deze kwestie hier opgenomen, binnen een uurtje aangepast.
Dat William Shakespeare niet de schrijver zou zijn van de werken die aan hem worden toegeschreven, is geen nieuwe theorie, maar het idee wordt door wetenschappers nauwelijks serieus genomen. Het bewijs dat Shakespeare wel degelijk de auteur is, is immers overweldigend. Het gedicht dat Van Egmond analyseert wordt door velen juist gezien als een bewijs daarvan gezien, want Jonson schrijft erin dat hij het vindt lijken op de man die hij kende.
Maar goed laten we eens kijken naar het gepuzzel van Van Egmond. In een document op zijn website [‘Shakespeare’ as metaphor; squaring the circle] heeft hij het allemaal net wat uitgebreider opgeschreven en het staat ook in zijn vorig jaar verschenen boek Homo universalis – Moreel kompas voor een nieuwe Europese renaissance.
De gravure die Martin Droeshout maakte voor de First Folio ziet er in onze ogen inderdaad wat raar uit, en heeft geleid tot complottheorieën, er zou een verborgen boodschap inzitten. Kunsthistorici hebben er echter niet zo’n probleem mee en wijzen op andere portretten die soortgelijke ‘fouten’ bevatten. Het idee dat het portret zo slecht is dat de samenstellers van de First Folio het alleen geaccepteerd zouden hebben als ze expliciet opdracht gegeven zouden om die verborgen boodschappen er in aan te brengen, kan dus eigenlijk gelijk de prullenbak in.
Hieronder nog eens geillustreerd hoe volgens Van Egmond hier tot twee keer toe een verwijzing naar het getal π in zou zitten, u weet wel de verhouding tussen de omtrek van een cirkel en zijn diameter (of τ/2 voor de liefhebbers). Dus 14 knoopjes beneden de scheiding die gevormd wordt door de rand van de kraag, en een vage 3 die je kunt ontwaren in de contouren van het gezicht: 3,14. Kan niet missen, toch?

Dan naar het gedicht van Ben Jonson. Het zou volgens Van Egmond een gebouw zijn dat verwijst naar Vitruvius, cirkels en vierkanten en het getal π. Om met dat laatste te beginnen: Van Egmond suggereert dat Jonson door te stellen dat er te weinig koper zou zijn om ‘This Figure’ helemaal tot zijn recht te laten komen, erop doelt dat de decimale ontwikkeling van π oneindig is. Nu is dat voor elk getal, alleen kunnen we bij rationale getallen, getallen die je als een breuk kunt schrijven, de ontwikkeling wel afkappen zonder aan precisie te verliezen, omdat er op een gegeven moment een herhaling optreedt. Bij irrationale getallen treedt er geen herhaling op en is de ontwikkeling in decimalen ‘willekeurig’.

Dat π een irrationaal getal is is echter pas in 1761 bewezen door Lambert (hoewel het al eerder werd vermoed door Euler), meer dan een eeuw na het verschijnen van de First Folio. In de tijd dat die uitkwam, bestond de beste benadering van π uit 35 decimalen, uitgerekend door Ludolph van Ceulen. Je ziet hiernaast een gravure van hem, waarbij zijn hoofd ook wel wat lijkt te zweven! Er moet hier vast ook een code in verborgen zitten, ik tel vier knoopjes… Maar het was in 1623 dus nog niet bekend of π misschien toch als breuk geschreven kon worden en de suggestie dat Jonson al wist van niet, is luchtfietserij.
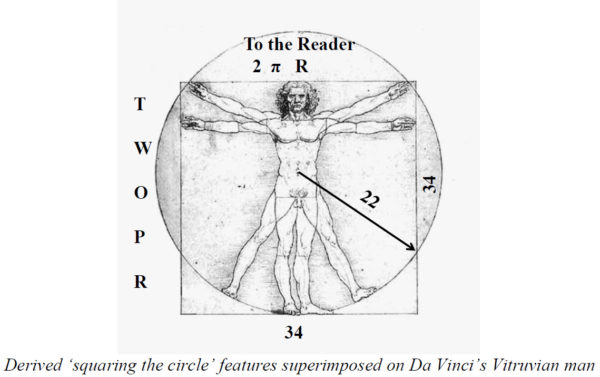
Dan zou het totaal aantal woorden in de wel en niet ingesprongen regels van het gedicht, telkens 34, duiden op een vierkant van 34 bij 34. Dat het getal 34 bij Jonson een bijzondere betekenis had en terugkomt in ander werk, zou best kunnen, daar heb ik geen idee van. Als Van Egmond echter verder gaat door erop te wijzen dat de omtrek van het vierkant van 34 bij 34, 136 dus, impliciet verwijst naar de bekende benadering 22/7 voor π, is ie me toch even kwijt. OK, een cirkel met omtrek 136 heeft als straal dan wel 21,6, afgerond 22, maar het geeft een minder goede benadering van π dan wanneer je zou starten met een vierkant van 35 bij 35. Merkwaardig. De ‘7’ uit de breuk 22/7 vind je overigens terug in het aantal woorden in de tekst die beginnen met een hoofdletter, maar niet aan het begin van een regel staan. Tuurlijk.
Ook merkwaardig is dat Van Egmond dit interpreteert als een verwijzing naar het bekende probleem van de kwadratuur van de cirkel. Dat is namelijk altijd gedefinieerd als het vinden van een vierkant met dezelfde oppervlakte als een gegeven cirkel, niet in termen van omtrekken.
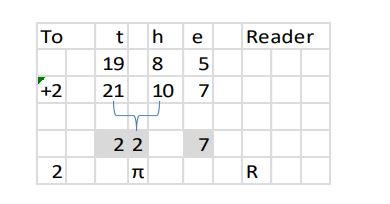
Tenslotte ziet Van Egmond aanwijzingen dat er een code in Caesar gescheimschrift in het gedicht is aangebracht. Het ‘To’ in de regel boven het gedicht moeten we lezen als ‘two’ wat een verschuiving inhoudt van twee letter in het alfabet, wat blijkbaar alleen toegepast moet worden op het volgende woord. Dat de ‘1’ van ’10’ bij de ’21’ die afkomt van’t’ moet worden opgeteld, en de ‘o’ dan als deelstreep moet worden gezien, is natuurlijk volstrekt helder. Ook dat deze symboliek zit in iedere tekst die begint met ‘To the Reader’…
In verticale richting ontwaart Van Egmond ook een ‘2πr’, daarvoor moet je naar de eerste letters van de niet ingesprongen tegels kijken: ‘T-W-O’, weer twee. Natuurlijk moet dat weer slaan op een verschuiving in de volgende niet ingesprongen regels, maar nu spring je niet in het alfabet maar ga in de regel zelf opzoek naar het volgende woord dat begint met een hoofdletter! Je vindt zo de ‘P’ van ‘Print’ en de ‘R’ van ‘Reader’. Maar wacht eens even, dat is maar een verschuiving van 1, toch? Kniesoor die daar op let, en heb je een betere verklaring voor die woorden die midden in een zin onverklaarbaar een hoofdletter hebben gekregen? Kijk toch naar het resultaat: ‘T-W-O-P-R’, duidelijk weer ‘2πr’, de omtrek van de cirkel!
Dat de letter π pas vanaf 1706 in gebruik is geraakt als symbool voor de verhouding van de omtrek van de cirkel en zijn straal (door William Jones), weet Van Egmond gelukkig wel. Maar dat is volgens hem geen probleem, want het symbool kom je al eerder tegen bij William Oughtred. Dat was echter in 1647 en hij gebruikte het als symbool voor de omtrek, dus eigenlijk als uitkomst van ‘2πr’.
Van Egmond ziet de uitkomst van zijn gepuzzel als bewijs dat ‘squaring the circle’ het centrale thema is in het werk van Shakespeare, opgevat als een ideaal van Vitruvius met een snufje Rozenkruizers. En dan is Shakespeare natuurlijk ook niet de echte auteur, maar eerder een ‘symbolische representant van de Rozenkruizersbeweging.’ Ik zie het hele geneuzel eerder als verder bewijs van iets anders…
Toevoeging
Het speelt niet echt een rol in de argumentatie van Van Egmond, maar hij geeft ook het volgende plaatje. Daarin plakt hij de maten van het vierkant en de cirkel die hij in het gedicht van Jonson denkt te zien, op de bekende tekening van Leonardo Da Vinci (die weer wel een rol speelt in het boek van Van Egmond). Maar als je het zelf gewoon even nameet, komt je er snel achter dat de straal van deze cirkel helemaal geen 22 is, maar ongeveer 20,9. De tekening van Da Vinci heeft ook niets te maken met het wiskundige probleem van de kwadratuur van de cirkel, de cirkel heeft hier een aanzienlijk grotere oppervlakte dan het vierkant.