Dat een samenzwering sneller uitkomt doordat een betrokkene uit de school klapt of per ongeluk zijn mond voorbij praat als er meer samenzweerders op de hoogte zijn, ligt voor de hand. Maar kun je ook berekenen hoe lang dat ongeveer duurt als je het aantal betrokkenen weet? Dr. David Robert Grimes denkt dat je dat aardig kunt schatten. Hij publiceerde een artikel waarin hij een formule afleidt die bijvoorbeeld als uitkomst geeft dat als NASA de maanlanding zou hebben gefaket, dat dan met 95 procent zekerheid binnen vier jaar publiek bekend zou zijn geworden. Een wiskundig bewijs dat grootschalige complotten niet geheim kunnen blijven?
Dit resultaat ging aardig snel het internet over. Nu konden skeptici ook met wiskundige precisie complotdenkers alle hoeken van de kamer laten zien. In de Volkskrant haalde het resultaat van Grimes zelfs de tweede pagina van de krant. Inclusief afbeelding van de formule!
Grimes is van origine natuurkundige en werkt als kankeronderzoeker aan de universiteit van Oxford. Daarnaast schrijft hij veel populaire stukken over wetenschap (onder meer columns in The Guardian), die vaak over skeptische onderwerpen gaan, bijvoorbeeld de antivaccinatiebeweging en ontkenning van klimaatopwarming. In 2014 ontving hij voor zijn schrijverij de John Maddox Prize for Standing up for Science. Het onderwerp complottheorieën is hem dus niet vreemd en met zijn achtergrond is het begrijpelijk dat hij er wel een uitdaging in zag om het kwantificeerbaar te maken.
In zijn artikel On the Viability of Conspiratorial Beliefs, dat verscheen in Open Access tijdschrijft Plos One, doet Grimes uit de doeken hoe hij aan zijn formule komt. Hij kijkt alleen naar het uitkomen van samenzwering door lekken, bewust of per ongeluk. Externe factoren die een complot aan het licht kunnen brengen, neemt hij niet mee – de uitkomsten van het model zullen gemiddeld dan ook nog een te positief beeld laten zien (vanuit het gezichtspunt van de geheimhouders).
De aanname van Grimes is dat de kans dat iemand in een jaar tijd lekt behoorlijk klein is en dat verschillende lekken onafhankelijk van elkaar optreden. En één lek is eigenlijk ook wel voldoende voor het openbaar worden. Een aangewezen methode om dat soort zeldzame voorvallen aan te pakken is om uit te gaan van een Poissonverdeling. De kans op tenminste één lek tot tijd t wordt dan gegeven door de formule L(t)= 1-e^(-tφ) waarin φ het verwachte aantal lekken is in één tijdsperiode (bijvoorbeeld per jaar). Je ziet aan deze formule dat als je t maar laat oplopen de e-macht heel erg klein wordt en L naar 1 kruipt (‘het complot komt bijna zeker uit’).
Voor één samenzweerder is dat simpel en voor meer is het niet veel lastiger. Dan moet je alleen die waarde φ aanpassen. Als je uitgaat van N op gelijke wijze lekkende samenzweerders dan wordt de kans dat er geen één lekt in een jaar gegeven door (1-φ)N, en de kans dat er minstens één lek is door 1-(1-φ)^N en die waarde neem je nu als nieuwe φ op in de formule*. Grimes noemt (1-φ) voor het gemak nog even ψ en neemt in plaats van een vaste waarde N een tijdsafhankelijke functie daarvoor, N(t). De samenzweringsuitlekformule wordt dan:
Waarom Grimes het aantal samenzweerders in de tijd wil kunnen variëren met die functie N(t) is eigenlijk wel goed te begrijpen. Als een complot dat ooit op een moment is uitgevoerd lang geheim blijft, zullen er samenzweerders uitvallen door overlijden. De kans op uitkomen wordt dan vervolgens kleiner, want er zijn minder potentiële lekkers. Grimes geeft nog twee formules van hoe N in de tijd zou kunnen veranderen. Voor een complot dat voortdurend ‘bijgehouden’ moet worden (zoals bijvoorbeeld het verborgen houden van een eenvoudige kuur voor kanker), lijkt een benadering waarin je N(t) constant houdt een logischer keuze.
Leuk zo’n theoretisch afgeleide formule, maar doet ie het ook wel echt? Grimes kijkt daarvoor naar drie samenzweringen die uitgekomen zijn: de NSA-affaire (klokkenluider Edward Snowden onthulde dat het afluisteren en onderscheppen van berichtenverkeer veel verder gaat dan iedereen had vermoed), het Tuskegee-syfilisonderzoek (dat liep vanaf 1932, de besmette deelnemers kregen niet te horen dat ze syfilis hadden en ook geen medicijnen toen die beschikbaar kwamen met de ontdekking van antibiotica) en de affaire rondom het forensisch laboratorium van de FBI (willens en wetens werden talloze getuigenissen afgelegd op basis van onbetrouwbare onderzoeksmethoden).
Op basis van de (min of meer) bekende tijd dat deze zaken verborgen bleven en verschillende schattingen voor het aantallen betrokkenen, komt Grimes tot een conservatieve schatting voor de kans dat een samenzweerder lekt. In zijn berekeningen is Grimes er bij deze voorbeelden van uitgegaan dat ze uitkwamen als de kans daarop groter of gelijk aan 50 procent was. Als je uitgaat van de gunstigste schatting voor de geheimhouding kom je volgens Grimes uit op een 0,0005 procent lekkans per jaar per samenzweerder.
Er is veel aan te merken op deze benadering en Grimes geeft zelf in het Discussion gedeelte van het artikel een hoop mitsen en maren aan. Zijn schattingen om het model te ijken en een redelijke waarde voor p te vinden zijn grof, maar dat maakt niet zoveel uit voor zijn belangrijkste conclusie dat omvangrijke samenzweringen altijd uitkomen. Hij concludeert op basis hiervan dat het bij vermeende samenzweringen als dat de klimaatopwarming een omvangrijk bedrog zou zijn van wetenschappers en dat de maanlanding een hoax is geweest, het onmogelijk is dat ze zo lang verborgen hadden kunnen blijven. En dus dat er geen sprake kan zijn van samenzweringen in die zaken.
De vraag is natuurlijk of dit model niet te veel toegespitst is op de drie voorbeelden die Grimes heeft uitgekozen. De waarden die Grimes daaruit afleidt verschillen nogal, en wat zouden de uitkomsten zijn als hij andere voorbeelden had genomen? En daarbij moet je bedenken dat het hier gaat om samenzweringen die zijn uitgekomen. Zijn die wel representatief voor alle samenzweringen? Ook voor die juist (nog) niet zijn geopenbaard.
Op Twitter merkte een aantal scherpe geesten op dat er toch ook iets fundamenteels mis moest zijn met Grimes’ benadering. De meest in het oog springende aanwijzing hiervoor is grafiek 1:
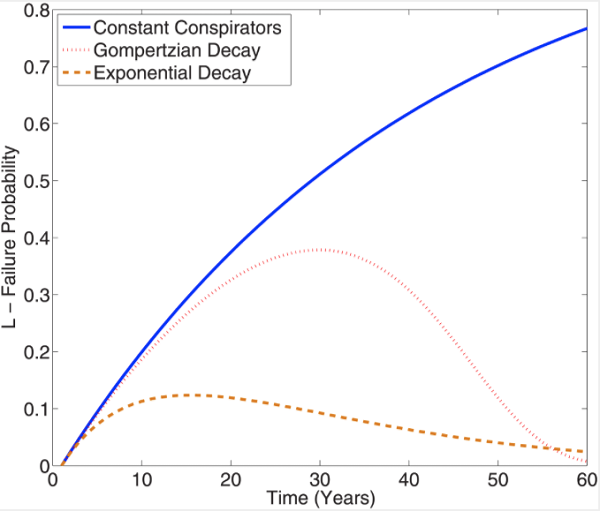Hierin zien we de drie verschillende scenario’s die Grimes in overweging neemt voor verloop van het aantal samenzweerders. De blauwe lijn is het scenario waar het aantal samenzweerders gelijk blijft, de roze stippellijn de situatie voor de gebeurtenis die geheim wordt gehouden door een groepje dat langzaam uitsterft door ouderdom, en de oranje stippellijn waarin het aantal samenzweerders elke zoveel jaar halveert. Telkens uitgaande van een startpopulatie van N=5000 en een lekkans van 0,0005 procent.
Deze grafiek zou de cumulatieve kans moeten weergeven dat het complot uitlekt. Maar een cumulatieve kans kan nooit gaan afnemen in de loop van de tijd, zoals bij de laatste twee scenario’s wel gebeurt! In de commentaren op Plos One bij het artikel vergelijkt iemand het treffend met een overlevingsgrafiek (dan moet je deze grafiek net verticaal omkieperen, naar de waarde 1-L kijken), waar geen stijging in kan voorkomen; dat zou er immers op duiden dat overledenen weer uit de dood opstaan (of in het geval van samenzweringen dat ze na openbaring weer geheim worden). Ik dacht dat Grimes misschien nog een slordigheidje had begaan bij het maken van deze grafiek (formule verwisseld ofzo), maar toen ik narekende bleek dat niet het geval te zijn – de formule is inderdaad dalend vanaf een bepaald tijdstip in de twee laatste scenario’s en dus heeft Grimes een probleem.
Dit ging waarschijnlijk mis omdat Grimes de formules voor het verloop van het aantal samenzweerders zomaar substitueerde in de formule die volgt uit de aanname dat het lekken Poisson verdeeld is. Die cumulatieve kansformule is echter afgeleid van de feitelijke kansverdeling en komt alleen op deze vorm uit als die factor in de exponent een constante is. Het vergt wat ver om dat hier helemaal in detail te laten zien, maar het komt er dus op neer dat Grimes de functie van het aantal samenzweerders in de tijd op een verkeerd niveau heeft ingevuld en daardoor verliest de door hem gevonden formule de relatie met het probleem dat die moet beschrijven. Als je het wel goed doet, komt die formule er waarschijnlijk ook stukken ingewikkelder uit te zien, maar ik heb dat niet uitgewerkt. Gelukkig voor Grimes lijkt het wel goed te gaan voor de gevallen waarin het aantal samenzweerders in de tijd gelijk blijft en dat zijn net de voorbeelden die hij verder uitwerkt.
Martin Robbins schreef hier wel een bijzonder kritisch stuk over: The maths of the paper disproving conspiracy theories don’t add up, waarin hij dit ook als een enorme blunder van de peer review bij Plos One benoemt. Er worden ook nogal wat mensen bedankt in het artikel die meegekeken hebben, en die hebben de fout dus ook niet opgemerkt. Robbins vindt het frustrerend dat dit artikel door skeptische organisaties en blogs als welkom resultaat is binnengehaald, vrolijk rondgetwitterd en anderszins verspreid:
It’s frustrating because a paper that lashes out against the idea that scientists might be engaged in covering up bad research turns out to be an example of bad research that slipped through peer review.
Robbins besluit gelukkig wat luchtiger:
Which leaves perhaps the biggest question of all: was this really just a bad paper, or was there some deeper purpose behind it? Is Doctor Grimes engaged in some kind of charade, running interference on behalf of a master or masters unknown? Is he still the real Grimes, or has he been replaced by a foppish-haired lizard impersonator? The truth is out there…
Het is ook een verwijzing naar de slotzin van Grimes’ artikel:
This work did not require specific funding, from nebulous clandestine cabals or otherwise.
In de commentaren op Plos One heeft Grimes zijn fout inmiddels ook al wel voorzichtig toegegeven. Hij is net op vakantie gegaan, dus ik neem aan dat een uitgebreidere reactie nog even op zich zal laten wachten.
* Toegevoegd (20:50 uur): hier gaat ‘t al mis, als N een constante is zou de correcte formule L(t)= 1-e^(-tNφ) worden. Grimes berekeningen kloppen ongeveer nog wel, maar dat komt alleen om dat bij deze hele lage lekkans p =0,0005 procent Np en (1-(1-p))^N elkaar niet veel ontlopen in de drie voorbeelden die Grimes analyseert. Bij de toepassing op de vermeende complotten waar hij uitgaat van honderdduizenden betrokkenen (bij die kuur voor kanker hanteert Grimes 714.000 – alle medewerkers van de acht grootste farmaceuten samen), zou de correcte formule nog veel eerder lekken voorspellen dan de formule van Grimes al doet.
Update 2 maart 2016: Plos One heeft inmiddels een correctie geplaatst van Grimes.
Steun Kloptdatwel
Waardeer je dit artikel? Je kunt onze site steunen met een financiële bijdrage. Dat waarderen wij dan weer! Een donatie kun je doen via dit betaalverzoek (of klik op de afbeelding hiernaast).
NB de rekening staat op naam van Maarten Koller, formeel eigenaar van deze site.
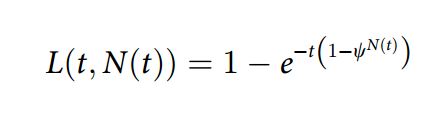
Een positief effect van dit verhaal is het zelfreinigende vermogen van de skeptische gemeenschap. Hoe vaak komt het voor dat in de alternatieve gemeenschap een onderzoek met positieve uitkomst zo snel door collega’s wordt ontkracht?
Nog een positief effect is dat er mijns inziens toch een kern van waarheid in het verhaal lijkt te zitten die verder onderzocht zou moeten worden. Daarbij zou je niet alleen kunnen kijken naar complotten, maar ook naar niet geheime zaken die toch heel lang de pers niet halen. Denk aan Bill Cosby of het kindermisbruik in de kerk of Jimmy Saville. Wanneer breekt iets door?
Wat ik mis in dit onderzoek is de optie dat in plaats van een gelijkblijvend of afnemend aantal mensen dat op de hoogte is van een complot of geheim, er juist steeds méér mensen op de hoogte raken van een geheim of complot. Mensen hebben de neiging iets belangrijks door te vertellen of krijgen last van hun geweten en gaan ergens te biecht. Je leest niet zelden “het gerucht werd steeds sterker dat …”.
Hoeveel studiemateriaal is er eigenlijk wel niet? Dan denk ik met name aan alle mensen in tv-studio’s die op hun klompen aanvoelen dat bijvoorbeeld Derek Ogilvie de boel belazerd? Zoals de editors die met knippen en plakken de pijnlijke missers moeten verhullen.
Hoe lang duurt het voordat zij uit de school klappen en wanneer breekt hun verhaal door of wanneer sterft het een stille dood? Of moeten we wachten tot ze gepensioneerd zijn en financieel onafhankelijk tot ze hun geheim loslaten? Zoals Fred Oster afgelopen week?
Zie hier niet zo de zin van in hoor. Meer iets voor als je teveel tijd hebt.
Wat bedoel je met ‘hier’?
Dat je wil gaan uitrekenen of lekkende mensen voorspelbaar zijn. Als iets de geschiedenis wel bewezen heeft is dat je nooit moet uitgaan van kansberekening en statistieken, denk maar aan de Engel des Doods (LdB), die foutief veroordeeld werd omdat de ‘odds’ tegen haar waren.
Noem eens één concreet voordeel van deze formule? Of is het toch een grote grap?
Maar goed, ik zal het wel weer helemaal verkeerd begrijpen?
Ik vind het geneuzel en ik kom er niet uit of het soms een grap is.
Vage berekeningen en tot welk concreet doel? Je kunt er niets mee, en het is al net zo vaag als de samenzweringen zelf.
Ben het met je eens Constantia. Alleen een formule die goed is te verifiëren heeft wetenschappelijke waarde
[ Alleen een formule die goed is te verifiëren heeft wetenschappelijke waarde ]
Dus je bent het gewoon eens met de inhoud van het bovenstaande artikel?
Nee natuurlijk niet. Welke data zijn er voorhanden om de formule te valideren? Die zijn er niet. Leuke theoretische exercitie. Wetenschappelijke waard: nul.
Er zijn drie gevallen waarop de formule is gebaseerd. Met die data van die drie gevallen kun je de formule verifiëren. En met data van niet gebruikte complotten die ook zijn uitgelekt.
Het was dus niet een louter theoretische exercitie.
De formule bleek echter niet geheel juist. De wetenschappelijke waarde is er toch echt wel, want het is een mooie basis voor nader onderzoek naar een betere formule.
3 gevallen, toe maar. Er zijn honderden artikelen die “aantonen” dat electromagnetische staling schadeljk is voor de gezondheid. En dat gelooft hier ook niemand. Omdat minstens zoveel onderzoeken het tegendeel “aantonen”. Evenzo voor de formule. Er zullen oneindig meer gevallen zijn waarin de formule niet dan wel klopt. En dus is de formule inderdaad niet juist. Welk complex probleem laat zich beschrijven met 2 parameters (phi en N)? Zo zit de wereld niet in elkaar. Daar kom je vanzelf achter als je fysische/biologische/maatschappelijke/etc. processen probeert te modelleren.
Ik denk niet dat er nader onderzoek komt.
[ 3 gevallen, toe maar. ]
Je bent toch niet verbaasd? of had je het artikel niet gelezen?
En die 3 casussen hebben niks te maken met het aantal onderzoeken, je vergelijking met ‘honderden artikelen’ over EMS gaat dan ook mank.
Of een probleem zich laat beschrijven met 2 parameters weet ik niet, maar ik ben wel verheugd dat je nu met argumenten komt in plaats van in te stemmen met iemand die het onderzoek met nul onderbouwing ‘zinloos tijdverspillend geneuzel’ noemt, dat mogelijk zelfs een grap is. Die vervolgens JWN complimenteert en hem de conclusie ‘geneuzel’ opdringt als hij nota bene met zijn commentaar eigenlijk aangeeft dat het absoluut zinvol is om over een formule na te denken.
Zijn er geen formules voor groepsprocessen? Wie stopte ook alweer de banen van de planeten in een formule, maar de afwijkingen in die banen schreef hij op het conto van God? en later was er iemand die het differentiaalrekenen of zo uitvond en toen pasten de planeetbanen wél in een formule.
Natuurlijk zijn er formules voor simpele processen als de kans dat je 6 keer achter elkaar een 6 gooit met een zuivere dobbelsteen. Bewegingen van planeten is ook een relatief simpel proces. Kepler had een makkie vergeleken met Grimes. Menselijk gedrag vangen in formules is nog niemand echt goed gelukt. Dat zijn namelijk niet-lineaire chaotisch processen. Ik weet niet waarop jouw vertrouwen in Grimes is gebaseerd, gegeven alleen al de tegenwerpingen op dit blogje. Of ben je het niet eens met de hier geuite kritiek?
Enter Martin Bier (wink)
Waar haal je vandaan dat ik vertrouwen in Grimes heb?
Van ‘het weer’ zeggen ze ook dat het chaotische processen zijn, toch? Die vlinder in Japan en zo? En toch kunnen ze een deel goed voorspellen.
Waarom zou dat niet met
menselijk gedraggroepsgedrag kunnen? Zijn formules hoe een file ontstaat geen groepsgedrag? Hoe vluchtende mensen uit meerdere nooduitgangen kiezen?[Waar haal je vandaan dat ik vertrouwen in Grimes heb?] Je eigen woorden: “….. want het is een mooie basis voor nader onderzoek naar een betere formule”. “mooie basis” is voor mij synoniem met dat je er wel heil in ziet.
Met de hier geuite kritiek ben je het dus inderdaad niet eens.
Het weer is inderdaad een chaotisch proces waardoor grootschalige weer fenomenen (hoge en lage drukgebieden) een maximale voorspelbaarheid hebben van 14 dagen. Kleinschalige fenomenen (thunderstorms, tornado’s, etc.) echter hebben een voorspeltermijn van slechts enkele uren.
Het ontstaan van files heeft vooral een grote correlatie met de weersomstandigheden en minder met groepsgedrag. Ik heb ook helemaal niet gezegd dat er geen modellen zijn voor groepsgedrag. Maar wel dat dergelijke modellen niet kunnen bestaan uit slechts 2 parameters. De wereld is complexer dan dat. Vandaar mijn wantrouwen in de niet tot nauwelijks gevalideerde formule van Grimes
[ “mooie basis” is voor mij synoniem met dat je er wel heil in ziet. ]
Voor jou.
oh, nou zie je er ineens geen heil meer in? Tegen zoveel inconsistentie kan ik niet op. Ik laat het hier maar bij.
Ik zie heil in een formule.
De incorrecte Grimes formule + de discussie lijken mij een mooie basis voor een betere formule.
Dat is mijn consistente standpunt, al vanaf het begin zo geweest, en daar zul je het mee moeten doen.
Het mensencollectief is in z’n doen en laten niet zelden bijna net zo voorspelbaar als de baan van een planeet. Zoek ze maar op: het model van Kermack en McKendrick voor het verloop van een epidemie, het model van Richardson voor een wapenwedloop en het model van Lanchester voor het verloop van een oorlog. Al die modellen en hun formules zijn net zo eenvoudig als dat ze accuraat gebleken zijn.
Het uitgangspunt van Grimes (constante verraadkans per jaar per samenzweringsbetrokkene) is heel redelijk. Steeds meer betrokkenen gaan natuurlijk dood en van daaruit berekent hij de cumulatieve uitlekkans van de samenzwering als functie van de tijd. Het is een heel aardige en originele opzet. Het is jammer dat Grimes met de wiskundige uitwerking zo gigantisch geblunderd heeft. Nu zal ie herinnerd worden om z’n blunder meer dan om het aardige idee. En verder het is een schande dat de referees van het artikel dit niet hebben gezien.
Inderdaad Martin, simpele modellen kunnen vaak heel illustratief zijn en eigenschappen van het fenomeen dat ze beschrijven blootleggen. Het probleem zit ‘m vaak in de aannames die gedaan moeten worden om het probleem in eenvoudige formules te kunnen vangen. Die aannames zijn vaak onrealistisch waardoor de bruikbaarheid van het model in de praktijk vaak tegenvalt.
Dat geldt vermoedelijk ook voor Grimes. Hoe gaat hij voor een willekeurig complot de beginwaarde van N, N(t=0), bepalen? Het zou leuk zijn als Grimes de kritiek opvat als uitdaging en de moed heeft zijn werk te verfijnen. Ik vermoed dat hij uiteindelijk iets meer nodig zal hebben dan een enkele vergelijking met 2 parameters.
Waar? Waar?! Echt niet! Dit zuig je per directo uit je duim!
En denk maar niet dat JW jou hieruit gaat redden!
Het aantal doelpunten in een voetbalwedstrijd – volgens velen een complex probleem- blijkt vrij nauwkeurig Poisson verdeeld te zijn, en wordt dus door 1 parameter, het gemiddelde aantal doelpunten per wedstrijd, beschreven. Natuurlijk moet je dat gemiddelde bepalen uit een zo groot mogelijk aantal waarnemingen (bij voorkeur meer dan 3…).
De verdeling van lichaamslengte, die tot stand komt in een complex biologisch proces en van vele factoren afhangt, is vrij nauwkeurig normaal verdeeld en wordt dus door 2 parameters, gemiddelde en variantie beschreven. Opnieuw, beiden te schatten uit een zo groot mogelijk aantal waarnemingen.
Ook fysische processen, bijvoorbeeld falen van machines of elektronische apparaten, kunnen met een beperkt aantal parameters worden gemodelleerd. Overigens had de bedenker van de formule waar het hierom gaat zich beter eerst kunnen verdiepen de bestaande theorie voor dit soort processen (reliability theory) want daarin spelen formules van dit type een centrale rol.
Ik snap niet wat je nu precies zeggen wilt.
Kun je de formule voor de verdeling van lichaamslengte (die totaal niet het directe gevolg van menselijk gedrag is) überhaupt vergelijken met een formule waarin
– de behoefte om belangrijke kennis te delen
– de behoefte een schoon geweten te hebben
– de fouten van het ‘je mond voorbij spreken’
– de neiging wraak te willen nemen
– de neiging roem te oogsten
– de neiging geld te willen verdienen
– de angst voor repercussies
en zo voorts een rol spelen?
Dit was een antwoord op de vraag in de post van Arie B: “Welk complex probleem laat zich beschrijven met 2 parameters”?
Omdat hij daarna stelt: “Zo zit de wereld niet in elkaar. Daar kom je vanzelf achter als je fysische/biologische/maatschappelijke/etc. processen probeert te modelleren”, dacht ik wat voorbeelden van die drie type processen aan te dragen die wel met twee parameters zijn te beschrijven.
Om mijn voorbeeld van een probabilistische formule voor het aantal doelpunten aan te halen, het gaat om de kansverdeling van het aantal doelpunten, wat een enkel getal is dat het gevolg is van een hele rij factoren,
– de neiging roem te oogsten
– de neiging geld te willen verdienen
– de neiging wraak te willen nemen
– angst voor de tegenstander
– de conditie van de grasmat
– etc etc
Grimes had ook als doel om het resultaat van een een heleboel drijfveren te reduceren tot de kansverdeling voor de tijd dat een complot nodig heeft om uit te komen.
Ik zie geen principiële reden waarom dat niet zou kunnen, zonder dat ik wil beweren dat *alle* processen met enkele parameters gemodelleerd kunnen worden.
Geert heeft het inderdaad niet zo begrepen. Het aantal doelpunten Poisson verdeeld. Kan. En dan? Kan Geert hiermee voetbaluitslagen voorspellen? Lijkt me niet. Een typisch geval van gemiddeld goed, maar bijna altijd fout voor ieder individueel geval. Dergelijke kennis heeft geen enkele voorspellende waarde.
En ja, de centrale limietstelling is vaak toepasbaar. Dit is geen nieuws.
Zo heb ik het inderdaad niet begrepen, maar meer zoals jij het stelt. Je voorspelt geen gebeurtenissen, maar kansen op gebeurtenissen.
Ik begrijp dat Grimes, door de Poisson limietstelling (verkeerd) toe te passen, beweringen wil kunnen doen als: de kans dat de maanlandingscomplot na 53 jaar nog niet is uitgekomen is, (laten we zeggen, bij gebrek aan de juiste formule) 0.1%. Kan best een complot zijn, maar waarschijnlijk is het niet.
In de meest strikte interpretatie “geen enkele voorspellende waarde”, maar toch zegt het in mijn oren meer dan ‘verwaarloosbare kans’ of ‘zeer onwaarschijnlijk’ of andere uitdrukkingen zoals de krant het liefst gebruikt.
Er klopt wel meer niet. In de eerste plaats was de uitleg in de Volkskrant van de formule fout. De uitleg die bij psi stond (kans dat iemand uit de school klapt) had moeten zijn ‘kans dat iemand in een jaar NIET uit de school klapt’, dus typisch iets van 0,999… in plaats van 0,000… Dat heb ik naar de krant geschreven, maar de krant heeft het niet afgedrukt. Een zo’n woordje vergeten, ach…
Voorts is het fout om de tijdafhankelijkheid van N op die manier te verwerken. Je moet die term tussen haakjes (nl. 1 min psi tot de macht N(t)) niet domweg vermenigvuldigen met t, maar integreren naar de tijd (nl. van 0 naar t). Als N constant is dan komt dat inderdaad neer op gewoon vermenigvuldigen met t, zoals in de formule.
Machiavelli schreef al over complotten. In zijn tijd gingen complotten kennelijk uitsluitend over moordaanslagen op vermoedelijk goed bewaakte hooggeplaatsten, en de corresponderende motieven wraak dan wel pogingen om zelf de macht te grijpen. Dus behoorlijk concrete doelen (dit in tegenstelling tot de doelen in fameuze samenzweringstheorieën). Volgens Machiavelli (1531) zou een complot met meer dan 3 of 4 deelnemers al uitlekken.
Dan over het Tuskegee experiment: lees eens
https://en.wikipedia.org/wiki/Tuskegee_syphilis_experiment
Al helemaal in het begin trok iemand zich terug omdat hij het er niet mee eens was. Waar een complot erin bestaat dat je iets geheim houdt voor het publiek omdat je iets verkeerds doet,
meenden de organisatoren van de proef dat ze niks verkeerds deden. In een RCT de placebo-allocatie geheim houden, wordt toch ook niet als verwerpelijke plannenmakerij gezien?
Een bekend complot dat het toch behoorlijk lang uithield zijn de pogingen van Big Tobacco om wetenschappelijke twijfel te zaaien aan de schadelijkheid van tabak.
Ook de georganiseerde misdaad is per definitie een complot. Dat heeft een merkwaardig aspect: ‘men’ weet best wie het gedaan heeft, alleen is juridisch sluitend bewijs niet rond te krijgen.
Diverse ‘hoaxes’ zijn ook complotten (met weinig deelnemers). Ik noem het Oera Linda Boek. In elk geval heeft niemand daar bekend. Een veel ernstiger hoax, de Protocollen van de Wijzen van Zion, daarvan is niet goed bekend wie het gedaan heeft (de Russische geheime dienst) en ook niet oorspronkelijk waarom (waarschijnlijk niet zozeer joden in het algemeen zwart maken, maar meer specifiek de Russische minister van financiën graaf Witte). Er zijn natuurlijk wel overvloedig bewijzen gevonden dat het een verzinsel was, maar niet doordat er een dader uit de school klapte.
Dank voor het onderbouw wat ik al zei: dit is *dus* geneuzel. Jammer dat je de Volkskrant niet haalde, shame on them.
Geneuzel is onzinnige praat. Maar praten over onzin, in dit geval praten over wat er niet klopt kan leiden tot nieuw inzicht. Dat is volgens mij de premisse van deze hele website.
Ik kreeg na wat heen en weer getweet met Jonathan Jones (die in de reacties op het artikel de fout heeft aangewezen, die intussen door Grimes en de ‘handling editor’ wel erkend is) het idee gekregen dat Grimes eigenlijk niet zo heel precies doorhad wat ie aan het doen was met die Poissonverdeling. Heel vaak wordt die gebruikt als benadering voor een Binomiale verdeling (gaat goed in het geval N*p<<1). In Grimes formule pakt het zo uit dat er een minimale uitkomsttijd (voor bepaalde keuze van L) is, hoe groot je N ook maakt. Als je uitgaat van uitkomen als L=50% dan zou het nooit sneller kunnen gaan dan een maand of vier. Dat kan nooit zijn bedoeling zijn geweest.
De juiste formule gebaseerd op een Poissonprocess met een tijd-variable verklapkans psi(t) (google: nonhomogeneous Poisson point process) is: L(t) = 1 – exp(-N*integraal_{0}^{t) psi(tau) d tau) voor t >=0 en anders 0. Omdat psi een kans is die per definitie niet negatief kan zijn, en ook t en N niet negatief zijn, is de integraal monotoon stijgend en daarmee L(t) dus ook.
Volgens mij is een formule voor hoe snel een complottheorie gemaakt wordt een stuk makkelijker: conspiracy pop up date = event date + 1 day
http://www.theguardian.com/world/2016/feb/04/alert-theres-a-dangerous-new-viral-outbreak-zika-conspiracy-theories
(Via Pepijn-Twitter)
Inmiddels heeft Plos One een correctie geplaatst van Grimes.
En opnieuw fout. Zoals je zelf terecht al opmerkte moet voor constante N de formule L(t)= 1-exp(-tNφ) worden. Grimes’ correctie levert voor N constant: L(t)= 1-exp(-t(1-(1-φ)^N)).