Dat een samenzwering sneller uitkomt doordat een betrokkene uit de school klapt of per ongeluk zijn mond voorbij praat als er meer samenzweerders op de hoogte zijn, ligt voor de hand. Maar kun je ook berekenen hoe lang dat ongeveer duurt als je het aantal betrokkenen weet? Dr. David Robert Grimes denkt dat je dat aardig kunt schatten. Hij publiceerde een artikel waarin hij een formule afleidt die bijvoorbeeld als uitkomst geeft dat als NASA de maanlanding zou hebben gefaket, dat dan met 95 procent zekerheid binnen vier jaar publiek bekend zou zijn geworden. Een wiskundig bewijs dat grootschalige complotten niet geheim kunnen blijven?
 Dit resultaat ging aardig snel het internet over. Nu konden skeptici ook met wiskundige precisie complotdenkers alle hoeken van de kamer laten zien. In de Volkskrant haalde het resultaat van Grimes zelfs de tweede pagina van de krant. Inclusief afbeelding van de formule!
Dit resultaat ging aardig snel het internet over. Nu konden skeptici ook met wiskundige precisie complotdenkers alle hoeken van de kamer laten zien. In de Volkskrant haalde het resultaat van Grimes zelfs de tweede pagina van de krant. Inclusief afbeelding van de formule!
Grimes is van origine natuurkundige en werkt als kankeronderzoeker aan de universiteit van Oxford. Daarnaast schrijft hij veel populaire stukken over wetenschap (onder meer columns in The Guardian), die vaak over skeptische onderwerpen gaan, bijvoorbeeld de antivaccinatiebeweging en ontkenning van klimaatopwarming. In 2014 ontving hij voor zijn schrijverij de John Maddox Prize for Standing up for Science. Het onderwerp complottheorieën is hem dus niet vreemd en met zijn achtergrond is het begrijpelijk dat hij er wel een uitdaging in zag om het kwantificeerbaar te maken.
In zijn artikel On the Viability of Conspiratorial Beliefs, dat verscheen in Open Access tijdschrijft Plos One, doet Grimes uit de doeken hoe hij aan zijn formule komt. Hij kijkt alleen naar het uitkomen van samenzwering door lekken, bewust of per ongeluk. Externe factoren die een complot aan het licht kunnen brengen, neemt hij niet mee – de uitkomsten van het model zullen gemiddeld dan ook nog een te positief beeld laten zien (vanuit het gezichtspunt van de geheimhouders).
De aanname van Grimes is dat de kans dat iemand in een jaar tijd lekt behoorlijk klein is en dat verschillende lekken onafhankelijk van elkaar optreden. En één lek is eigenlijk ook wel voldoende voor het openbaar worden. Een aangewezen methode om dat soort zeldzame voorvallen aan te pakken is om uit te gaan van een Poissonverdeling. De kans op tenminste één lek tot tijd t wordt dan gegeven door de formule L(t)= 1-e^(-tφ) waarin φ het verwachte aantal lekken is in één tijdsperiode (bijvoorbeeld per jaar). Je ziet aan deze formule dat als je t maar laat oplopen de e-macht heel erg klein wordt en L naar 1 kruipt (‘het complot komt bijna zeker uit’).
Voor één samenzweerder is dat simpel en voor meer is het niet veel lastiger. Dan moet je alleen die waarde φ aanpassen. Als je uitgaat van N op gelijke wijze lekkende samenzweerders dan wordt de kans dat er geen één lekt in een jaar gegeven door (1-φ)N, en de kans dat er minstens één lek is door 1-(1-φ)^N en die waarde neem je nu als nieuwe φ op in de formule*. Grimes noemt (1-φ) voor het gemak nog even ψ en neemt in plaats van een vaste waarde N een tijdsafhankelijke functie daarvoor, N(t). De samenzweringsuitlekformule wordt dan:
Waarom Grimes het aantal samenzweerders in de tijd wil kunnen variëren met die functie N(t) is eigenlijk wel goed te begrijpen. Als een complot dat ooit op een moment is uitgevoerd lang geheim blijft, zullen er samenzweerders uitvallen door overlijden. De kans op uitkomen wordt dan vervolgens kleiner, want er zijn minder potentiële lekkers. Grimes geeft nog twee formules van hoe N in de tijd zou kunnen veranderen. Voor een complot dat voortdurend ‘bijgehouden’ moet worden (zoals bijvoorbeeld het verborgen houden van een eenvoudige kuur voor kanker), lijkt een benadering waarin je N(t) constant houdt een logischer keuze.
Leuk zo’n theoretisch afgeleide formule, maar doet ie het ook wel echt? Grimes kijkt daarvoor naar drie samenzweringen die uitgekomen zijn: de NSA-affaire (klokkenluider Edward Snowden onthulde dat het afluisteren en onderscheppen van berichtenverkeer veel verder gaat dan iedereen had vermoed), het Tuskegee-syfilisonderzoek (dat liep vanaf 1932, de besmette deelnemers kregen niet te horen dat ze syfilis hadden en ook geen medicijnen toen die beschikbaar kwamen met de ontdekking van antibiotica) en de affaire rondom het forensisch laboratorium van de FBI (willens en wetens werden talloze getuigenissen afgelegd op basis van onbetrouwbare onderzoeksmethoden).
Op basis van de (min of meer) bekende tijd dat deze zaken verborgen bleven en verschillende schattingen voor het aantallen betrokkenen, komt Grimes tot een conservatieve schatting voor de kans dat een samenzweerder lekt. In zijn berekeningen is Grimes er bij deze voorbeelden van uitgegaan dat ze uitkwamen als de kans daarop groter of gelijk aan 50 procent was. Als je uitgaat van de gunstigste schatting voor de geheimhouding kom je volgens Grimes uit op een 0,0005 procent lekkans per jaar per samenzweerder.
Er is veel aan te merken op deze benadering en Grimes geeft zelf in het Discussion gedeelte van het artikel een hoop mitsen en maren aan. Zijn schattingen om het model te ijken en een redelijke waarde voor p te vinden zijn grof, maar dat maakt niet zoveel uit voor zijn belangrijkste conclusie dat omvangrijke samenzweringen altijd uitkomen. Hij concludeert op basis hiervan dat het bij vermeende samenzweringen als dat de klimaatopwarming een omvangrijk bedrog zou zijn van wetenschappers en dat de maanlanding een hoax is geweest, het onmogelijk is dat ze zo lang verborgen hadden kunnen blijven. En dus dat er geen sprake kan zijn van samenzweringen in die zaken.
De vraag is natuurlijk of dit model niet te veel toegespitst is op de drie voorbeelden die Grimes heeft uitgekozen. De waarden die Grimes daaruit afleidt verschillen nogal, en wat zouden de uitkomsten zijn als hij andere voorbeelden had genomen? En daarbij moet je bedenken dat het hier gaat om samenzweringen die zijn uitgekomen. Zijn die wel representatief voor alle samenzweringen? Ook voor die juist (nog) niet zijn geopenbaard.
Op Twitter merkte een aantal scherpe geesten op dat er toch ook iets fundamenteels mis moest zijn met Grimes’ benadering. De meest in het oog springende aanwijzing hiervoor is grafiek 1:
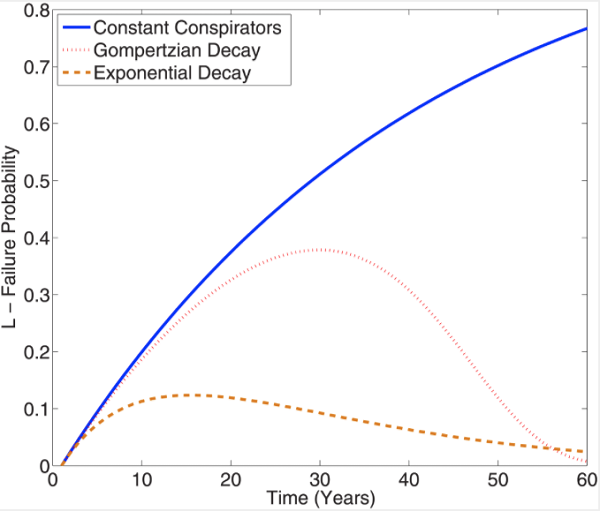 Hierin zien we de drie verschillende scenario’s die Grimes in overweging neemt voor verloop van het aantal samenzweerders. De blauwe lijn is het scenario waar het aantal samenzweerders gelijk blijft, de roze stippellijn de situatie voor de gebeurtenis die geheim wordt gehouden door een groepje dat langzaam uitsterft door ouderdom, en de oranje stippellijn waarin het aantal samenzweerders elke zoveel jaar halveert. Telkens uitgaande van een startpopulatie van N=5000 en een lekkans van 0,0005 procent.
Hierin zien we de drie verschillende scenario’s die Grimes in overweging neemt voor verloop van het aantal samenzweerders. De blauwe lijn is het scenario waar het aantal samenzweerders gelijk blijft, de roze stippellijn de situatie voor de gebeurtenis die geheim wordt gehouden door een groepje dat langzaam uitsterft door ouderdom, en de oranje stippellijn waarin het aantal samenzweerders elke zoveel jaar halveert. Telkens uitgaande van een startpopulatie van N=5000 en een lekkans van 0,0005 procent.
Deze grafiek zou de cumulatieve kans moeten weergeven dat het complot uitlekt. Maar een cumulatieve kans kan nooit gaan afnemen in de loop van de tijd, zoals bij de laatste twee scenario’s wel gebeurt! In de commentaren op Plos One bij het artikel vergelijkt iemand het treffend met een overlevingsgrafiek (dan moet je deze grafiek net verticaal omkieperen, naar de waarde 1-L kijken), waar geen stijging in kan voorkomen; dat zou er immers op duiden dat overledenen weer uit de dood opstaan (of in het geval van samenzweringen dat ze na openbaring weer geheim worden). Ik dacht dat Grimes misschien nog een slordigheidje had begaan bij het maken van deze grafiek (formule verwisseld ofzo), maar toen ik narekende bleek dat niet het geval te zijn – de formule is inderdaad dalend vanaf een bepaald tijdstip in de twee laatste scenario’s en dus heeft Grimes een probleem.
Dit ging waarschijnlijk mis omdat Grimes de formules voor het verloop van het aantal samenzweerders zomaar substitueerde in de formule die volgt uit de aanname dat het lekken Poisson verdeeld is. Die cumulatieve kansformule is echter afgeleid van de feitelijke kansverdeling en komt alleen op deze vorm uit als die factor in de exponent een constante is. Het vergt wat ver om dat hier helemaal in detail te laten zien, maar het komt er dus op neer dat Grimes de functie van het aantal samenzweerders in de tijd op een verkeerd niveau heeft ingevuld en daardoor verliest de door hem gevonden formule de relatie met het probleem dat die moet beschrijven. Als je het wel goed doet, komt die formule er waarschijnlijk ook stukken ingewikkelder uit te zien, maar ik heb dat niet uitgewerkt. Gelukkig voor Grimes lijkt het wel goed te gaan voor de gevallen waarin het aantal samenzweerders in de tijd gelijk blijft en dat zijn net de voorbeelden die hij verder uitwerkt.
Martin Robbins schreef hier wel een bijzonder kritisch stuk over: The maths of the paper disproving conspiracy theories don’t add up, waarin hij dit ook als een enorme blunder van de peer review bij Plos One benoemt. Er worden ook nogal wat mensen bedankt in het artikel die meegekeken hebben, en die hebben de fout dus ook niet opgemerkt. Robbins vindt het frustrerend dat dit artikel door skeptische organisaties en blogs als welkom resultaat is binnengehaald, vrolijk rondgetwitterd en anderszins verspreid:
It’s frustrating because a paper that lashes out against the idea that scientists might be engaged in covering up bad research turns out to be an example of bad research that slipped through peer review.
Robbins besluit gelukkig wat luchtiger:
Which leaves perhaps the biggest question of all: was this really just a bad paper, or was there some deeper purpose behind it? Is Doctor Grimes engaged in some kind of charade, running interference on behalf of a master or masters unknown? Is he still the real Grimes, or has he been replaced by a foppish-haired lizard impersonator? The truth is out there…
Het is ook een verwijzing naar de slotzin van Grimes’ artikel:
This work did not require specific funding, from nebulous clandestine cabals or otherwise.
In de commentaren op Plos One heeft Grimes zijn fout inmiddels ook al wel voorzichtig toegegeven. Hij is net op vakantie gegaan, dus ik neem aan dat een uitgebreidere reactie nog even op zich zal laten wachten.
* Toegevoegd (20:50 uur): hier gaat ‘t al mis, als N een constante is zou de correcte formule L(t)= 1-e^(-tNφ) worden. Grimes berekeningen kloppen ongeveer nog wel, maar dat komt alleen om dat bij deze hele lage lekkans p =0,0005 procent Np en (1-(1-p))^N elkaar niet veel ontlopen in de drie voorbeelden die Grimes analyseert. Bij de toepassing op de vermeende complotten waar hij uitgaat van honderdduizenden betrokkenen (bij die kuur voor kanker hanteert Grimes 714.000 – alle medewerkers van de acht grootste farmaceuten samen), zou de correcte formule nog veel eerder lekken voorspellen dan de formule van Grimes al doet.
Update 2 maart 2016: Plos One heeft inmiddels een correctie geplaatst van Grimes.
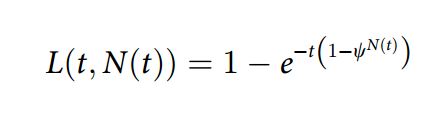
 Op het meest recente Skepsiscongres was het thema samenzweringen. Hoewel het bestaan van echte samenzweringen niet ontkend kan worden, zijn ook veel beweringen over samenzweringen aantoonbare onzin en voorbeelden van paranoia. Rond de aanvallen van 9/11 is een hele industrie van samenzweringstheoretici ontstaan (de zogenaamde ‘truthers’), die 9/11 zien als een actie van president Bush en de zijnen om een aanleiding voor een oorlog te verkrijgen. De mythes hieromtrent zijn behoorlijk hardnekkig (zie bijvoorbeeld
Op het meest recente Skepsiscongres was het thema samenzweringen. Hoewel het bestaan van echte samenzweringen niet ontkend kan worden, zijn ook veel beweringen over samenzweringen aantoonbare onzin en voorbeelden van paranoia. Rond de aanvallen van 9/11 is een hele industrie van samenzweringstheoretici ontstaan (de zogenaamde ‘truthers’), die 9/11 zien als een actie van president Bush en de zijnen om een aanleiding voor een oorlog te verkrijgen. De mythes hieromtrent zijn behoorlijk hardnekkig (zie bijvoorbeeld