Een ANP-bericht met als kop ‘Kwart van slimme vwo’ers niet in 6 jaar klaar’ werd donderdag 14 juni op veel nieuwssites klakkeloos overgenomen (onder andere de Volkskrant, Trouw, Nu.nl). De argeloze lezer krijgt snel de indruk dat er een specifiek probleem is voor de slimmerds en dat ze het misschien nog wel slechter doen dan hun medeleerlingen die met een lagere CITO-score aan het VWO begonnen. De onderzoekers spreken namelijk over een ‘schrikbarend hoog’ percentage. Het klinkt in eerste instantie nogal verontrustend, maar ik had er niet meteen een beeld bij. Is dat kwart nou veel meer dan je mag verwachten? Is het echt zo dramatisch? Het is maar hoe je ernaar kijkt.
Merkwaardig genoeg trof ik in geen van de berichten een link of anderszins bruikbare verwijzing naar het echte onderzoek. Het knippen en plakken van ANP-berichten heeft natuurlijk ook weinig met journalistiek te maken, maar het valt toch steeds weer op dat er werkelijk geen enkele moeite wordt gedaan om zo’n bericht van wat achtergrond en nuance te voorzien. Geen van de sites die het bericht overnamen zal vermoedelijk het rapport zelf gezien hebben. Het kostte mij niet veel moeite om het te vinden: eerst even kijken bij het onderzoeksbureau dat het uitvoerde (GION): nee, niets. Dan maar bij de opdrachtgever, het ministerie van OCW. En daar staat het dan, een stevig rapport van 118 pagina’s.
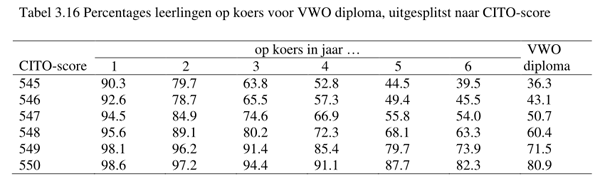
Er staat erg veel in, maar mijn oog viel snel op tabel 3.16 (blz. 36):
De tabel behoeft volgens mij weinig toelichting. De CITO-scores van 549 en 550 werden in het onderzoek opgevat als ‘excellent’. Een score van 545 is wel zo’n beetje de laagste waarmee je het VWO in kunt gaan. Ik zie hier weinig verontrustends aan, de tabel beantwoordt wel aan de verwachting die ik vooraf had. Misschien dat de percentages van alle CITO-score groepen wat beter kunnen, maar van een verontrustend beeld specifiek voor de ‘excellente’ groepen lijkt mij geen sprake. Hoe komen de onderzoekers daar dan bij? Dat wordt duidelijk als je wat verder bladert in het rapport. Op blz. 93 geven ze hun definitie van onderpresteren:
Wij hebben de (normatieve) opvatting gehanteerd dat het niet na zes jaar hebben behaald van het VWO-diploma als criterium voor ‘ondermaats presteren’ kan gelden.
Ja, zo kan ik het ook! Élke uitval wordt geïnterpreteerd als onderpresteren. Het gaat bijna zo ver dat ook uitval door overlijden als onderpresteren wordt beschouwd. In de percentages wordt daar gelukkig wel voor gecorrigeerd en het zal ook wel voor bovenstaande tabel zijn gebeurd. Maar er is geen correctie voor andere oorzaken van vertraging zoals ziekte en familieomstandigheden. Niet dat dat iets zal uitmaken voor de verhouding tussen de uitval van excellente en minder excellente leerlingen, maar het nuanceert wel dat ‘kwart van de slimmerds’ die niet in zes jaar het VWO doorloopt. Je hebt zo nog geen idee wat het terrein is dat überhaupt gewonnen kan worden door veranderingen in het onderwijs.

Vervolgens gaan de onderzoekers ijverig op zoek in de data om te kijken of er verschillen zijn te ontdekken tussen de groep excellente leerlingen die wel in zes jaar door het VWO fietst en de groep excellente leerlingen die ergens hapert. Dan wordt het wel snel data-vissen en moet je erg oppassen niet toevallige correlaties aan te treffen. We moeten ook bedenken dat alles is gebaseerd op een steekproef onder VWO’ers uit maar één startjaar, 1999. Ik zie niet al te veel slagen om de arm bij het vinden van de ‘oorzaken’ en de relevantie voor het onderwijs van nu.
Zo adviseren de onderzoekers om excellente leerlingen niet in gemengde HAVO/VWO klassen te laten beginnen, dat zou die excellente leerlingen 10% minder kans geven op een vlekkeloze doorstroom. Nou vraag ik me meteen af of die leerlingen niet om een heel goede reden gekozen hebben voor zo’n gemengde brugklas, maar de onderzoekers blijkbaar niet. Ook een gebrek aan ‘ordelijkheid’ wordt aangevoerd als een hindernis, maar dat kan net zo goed voor alle leerlingen gelden en niet specifiek voor de slimmerds (voor de gemiddelde groep wordt het niet als risicofactor gezien).
Kortom, het lijkt me weer een mooi staaltje naar de gewenste uitkomst toe redeneren. Natuurlijk moet er wat gedaan worden om te voorkomen dat onze toekomstige toppers onderweg een keertje struikelen. Anders blijft dat potje van 30 miljoen per jaar voor hoogbegaafde en excellente leerlingen ook maar ongebruikt op het ministerie staan …

Deze vind ik erg grappig; ik heb heel erg diep moeten nadenken wanneer ik voor het laatst een ordelijke tiener heb gezien. Maar raar genoeg is het gebrek aan ordelijkheid alleen bij de slimme tieners een probleem en kunnen de niet-zo-slimme er blijkbaar goed mee omgaan. Is het nu een bewijs van domheid of slimheid als je geen last hebt van je eigen slordigheid?
Misschien heb ik het niet zo duidelijk opgeschreven, maar bij de ‘niet-zo-slimme’ groep werd het door de onderzoekers niet als een risico factor gezien en dus niet uitgezocht. Waarschijnlijk hebben ze er net zoveel ‘last’ van als de excellente groep.
Dankjewel Pepijn.
Dat lijkt mij ook.
Had een reactie geplaatst maar die komt niet door.
Er is natuurlijk altijd zoiets als regressie naar het gemiddelde. Dat klinkt geleerd, maar het doet zich voor in elke situatie dat er tussen twee getalsmatig uit te drukken verbanden een niet-perfect statistisch verband is.
In dit geval gaat het om enerzijds de CITO-score en anderzijds de doorstroomsnelheid, of beter gezegd de duur van de opleiding.
De CITO-score is een momentopname. Die is niet zo precies als bijvoorbeeld ‘de lichaamslengte in millimeters op de 18de verjaardag, gemeten direct na het wakker worden’. Bij examens is het heel gebruikelijk dat de correlatie tussen een eerste examen en een tweede examen niet perfect is. Dat zal bij de CITO-toets niet anders zijn. Bij IQ-tests is die correlatie bijvoorbeeld naar ik meen ergens tussen 0,8 en 0,9.
Met andere woorden als je dezelfde leerlingen een maand of wat later nog eens zo’n toets zou laten doen, zou de score in een flink aantal gevallen een paar punten omhoog of omlaag kunnen gaan.
Dat de CITO-toets geen perfecte score is van het studietempo kun je inzien door even te kijken naar de laagste score waarmee je nog een vwo-advies krijgt: ruim een derde van die groep slaagt gewoon na zes jaar voor het vwo-examen. Je kunt dus denken dat ook voor CITO-scores 540-544 er nog een niet-verwaarloosbare kans is dat ze het vwo aankunnen, en zelfs dat ze het gewoon in zes jaar kunnen doen. Wat vind je van de krantenkop ‘Kwart havo-leerlingen kan waarschijnlijk best vwo aan’?
In het algemeen is het effect van matige overeenstemming tussen twee maten (hier CITO-score en vwo-cursusduur) dat het voor de ‘gemiddelde’ groep niet veel uitmaakt. De groep die gemiddeld scoort voor de ene maat zal bij de andere maat hetzelfde gemiddelde opleveren. Als je echter een extreme groep voor de ene maat bekijkt, zal die in de andere maat minder extreem afwijken van het gemiddelde, en de verhouding tussen beide afwijkingen van het gemiddelden is wat we de correlatiecoëfficiënt noemen. Je zou denken dat die correlatiecoëfficiënt dan per afwijking verschilt, maar dat is vaak niet zo.
In termen van IQ-tests: een correlatie van 0,85 tussen test en hertest houdt concreet in dat een groep die bij een eerste test allemaal precies 120 scoort, bij een tweede test uiteenlopende resultaten haalt, maar gemiddeld 3 punten minder. Daarentegen zal een groep die bij de eerste test 80 gemiddeld scoort, bij een tweede test uiteenlopende resultaten halen, maar gemiddeld 3 punten meer.
Die relatie is zelfs symmetrisch. Als je een tabel zou maken met links aantal jaren om vwo te voltooien (dus 6, 7, 8,… nooit) en rechts de gemiddelde CITO-scores van de groep, dan zou je rechts een rijtje krijgen dat beslist niet van 550 daalt naar 545, maar van bijvoorbeeld 548,… naar 546,…
Weer in termen van IQ-tests: als je een grote toevallig gekozen groep mensen tweemaal test en je zoekt degenen uit die bij de tweede test 120 gescoord hebben, dan zal (weer bij correlatie 0,85) die club bij de eerste test uiteenlopende resultaten gehad hebben, maar gemiddeld 117, dus 3 punten minder.
Sommige mensen denken dat regressie naar het gemiddelde een mysterieus proces is dat maakt dat we allemaal in alle opzichten steeds mediocrerder waoren maar dat is niet zo. Het is een gevolg van het feit dat statistische verbanden tussen de dingen nu eenmaal zelden perfect zijn
De voor de hand liggende verklaring is natuurlijk dat je van een twaalfjarige aan de hand van een enkele momentopname op één school niet kunt voorspellen hoe die de volgende zes jaar lang gaat presteren op een andere school waar de lat een stuk hoger ligt, en waar de vakken ook totaal anders zijn.
Het is natuurlijk lastig om zulke algemeenheden toe te passen op dit geval omdat je nu eenmaal geen vwo-studieduren kunt bepalen voor alle groepen van CITO-score 501 tot 550. Maar ik zie, waarschijnlijk met Pepijn, niets anders dan regressie naar het gemiddelde, anders gezegd, de matige voorspellende kracht van tests in het algemeen.
Die vind ik mooi gevonden!
Nog een kleine toevoeging: het rapport spreekt over ‘excellente’ leerlingen. Bedoeling was de 5% ‘slimste’ in de een of andere zin. Daarom legt men de lat bij score 548 (top 7,4%) of 549 (4,4%). In IQ-termen is dat 120-125.
Zien ook het histogram in het rapport op pagina 8.
(Toen ik naar school ging, waren er publicaties die beweerden dat gymnasium en HBS bedoeld waren voor IQ boven de 130, en in die tijd deed maar 1 op 4 -of 1 op 10, dat ben ik vergeten – de opleiding in de minimumtijd, en zeker de helft van de eersteklassertjes haalde nooit de eindstreep.
Kinderen testen heeft inderdaad een matige voorspellende kracht en vind ik dus dat er teveel waarde wordt gehecht aan o.a. de Cito-toets.
Ik heb de nodige kinderen zien beginnen op het Vwo om terug te zakken naar de Havo en zelfs de Mavo. Anderom kan ook. Volgens de Cito-score moeite met Vbo, maar ouder zag dat anders en het werd de Mavo. Daarna naar de Havo en Hogeschool om na een jaar met behoorlijk hoge punten de propedeuse op zak te hebben, dus de deur open voor de Universiteit.
Kortom: ik houd niet zo van etiketjes plakken op basis van een momentopname.
Tja, ook dit zijn natuurlijk anekdotes. Persoonlijk had ik een CITO-score van 549. Ik zou VWO dus moeten kunnen. Een CITO houdt echter geen rekening met motivatie en puberaal gedrag, dus dat werd HAVO met blijven zitten in de eindexamen klas. Mijn houding was ‘waarom zou VWO me boeien? Ik ga toch nooit naar de universiteit’… ik ben toch erg blij dat ik daar uiteindelijk wel terecht ben gekomen. Maar uiteindelijk bleek voor mij dat mijn CITO-score bij mijn capaciteiten paste. Maar twee jaar na de CITO-toets zou je me toch echt heel anders hebben ingeschat.
Over het algemeen is een CITO naar mijn mening dus prima in staat iets te zeggen over de capaciteiten van een kind. Maar dat is een mening en ik heb me nooit verdiept in de onderzoeksresultaten of dat echt zo is. Tot dan is voor elke anekdote wel ergens een tegen-anekdote te halen.
2012/7/4 Disqus
Wat voor een raar schaal van deze CITO-toets? Van 501 tot 550. Ik heb al geprobeerd de wikipedia te raadplegen, maar ik heb het eigenlijk niet echt begrepen. Waar is het cijfer 5 goed voor dat altijd voor de eigenlijke uitslag wordt geschreven?
Nu heb ik me vandaag net een beetje met het Nederlands onderwijs-stelsel bezig gehouden. Het lijkt me ontzettend ingewikkeld, temeer omdat de uitleggen zo veel afkortingen bevatten.
Voor zover ik het begrijp is voor deze schaal gekozen om de indruk weg te nemen dat het om een proefwerk of een IQ-test zou gaan.
http://nl.wikipedia.org/wiki/Cito_Eindtoets_Basisonderwijs
Doe je het snel, is het wéér niet goed. Dit vind ik dus écht niet kunnen – al wil iemand een vier-zes jarige studie in drie maanden doen, dan nog moet dat kunnen en juist beloond worden in plaats van bestraft:
http://www.ad.nl/ad/nl/1014/Bizar/article/detail/3280989/2012/07/03/Kortstudeerdersboete-voor-te-ijverige-Duitse-student.dhtml
Dat vind ik dus ook Constantia met hun ”’we lopen collegegeld mis'”zijn ze helemaal gek geworden?
Nu moet hij het wel alsnog betalen.
artikel in Der Spiegel
Vreemd !
Dat valt me tegen van die Duitse rechter.
Nooit zo’n snel antwoord gekregen, amper 2 minuten. Ik heb het artikel zelf nog niet gelezen. Ik ga er straks mee aan de slag.
Ondanks mijn luiheid ben ik af en toe heel snel. 😉 Ik kreeg een mailtje dat er een reactie was geplaatst en ik reageerde meteen.
De regressie naar het gemiddelde lijkt een verbluffend effect te zijn. Ik kende dat tot nu niet, maar als je daar een beetje over nadenkt schijnt het toch een logisch gevolg te zijn. Ik probeer het maar met woorden uit te leggen aan de hand van een simpel voorbeeld.
Uit een grote groep proefpersonen kijken wij naar drie groepen. Groep A zijn degene die gemiddeld een score van 115 zouden behalen als ze maar vaak genoeg aan zo’n IQ-test meedoen. Maar soms scoren ze ook 110 of 120. Groep B zijn degene die gemiddeld 120 scoren en groep C 125. En nu vormen we nog een 4de groep, ik noem die maar groep X, dat zijn degene die allemaal bij één bepaalde test precies 120 hebben gescoord. Wie zit er nu precies in, in deze groep? Het merendeel komt natuurlijk uit groep B (maar niet alle van B), een bepaalde percentage uit groep A en ruim dezelfde percentage uit groep C.
En nu komt de oplossing voor het verschrijnsel: Groep A is tamelijk wat groter dan groep C, denk aan de klok-coerve van Gauss. Dus de “geleende” personen uit A zijn meer dan de “geleende” uit C. Het meerendeel van deze geleende scores moeten later bij een volgende test (alleen met groep X !) weer worden teruggegeven, dus de gemiddelde score daalt een beetje. Bedenk ook dat je groep A, B en C enerzijds en groep X anderzijds niet zomaar met elkaar kunt vergelijken.
Je kunt het ook ‘grafisch’ bekijken. Je geeft iedereen twee tests. Ze krijgen dus allemaal twee uitslagen, bijvoorbeeld (115, 120) of (70, 71) of (85, 76). Die getallenparen breng je in grafiek. Je krijgt dan een puntenwolk, die symmetrisch ligt ten opzichte van de lijn y=x. (Als de kandidaten bij de eerste test handigheden hebben opgestoken die ze bij de tweede test kunnen gebruiken, dan klopt die symmetrische ligging niet.)
Als je dit met andere variabelen (bijvoorbeeld armlengte en beenlengte) doet, moet je wel zorgen dat je de uitkomsten zo normeert dat de zgn. standaarddeviatie van de variabelen gelijk is, anders is de helling van de hoofdas van de wolk de verhouding van de standaarddeviaties. Ook moeten de gemiddelden gelijk zijn, anders klopt de helling van de symmetrielijn wel, maar gaat die lijn niet door het punt (0,0).
Denk je de puntenwolk nu even vereenvoudigd tot een ellips. Als de test en hertest goed met elkaar overeenstemmen dan is die ellips een soort lange sigaar. Maar bij slechte overeenstemming is de wolk nogal rond.
Nu ga je voor elke x het gemidelde van alle bijbehorende y bepalen. Vanwege ons vereenvoudigde model is dat eenvoudig. De verticale lijn die bij zo’n x hoort snijdt de ellips in twee punten. Het gezochte gemiddelde corresponeert met het midden tussen die twee punten.
Het mooie (van ellipsen, cirkels en zelfs parabolen en hyperbolen) is dat als je dat voor elke x doet al die middelpunten op een rechte lijn liggen! (Vergeet die maffe statistiek en zoek uit waarom dat zo is, dat is toch vééél interessanter, dat is echte 100% betrouwbare meetkundige kennis.) Uiteraard zal die lijn verlopen tussen de twee punten waar de ellips een verticale raaklijn heeft.
Dat is nou de regressielijn (van y op x). De helling is de correlatiecoëfficiënt (als je goed genormeerd hebt, zodat y=x de hoofdas van de ellips is).
Het is duidelijk dat tamelijk ronde wolk = kleine correlatie-coeëfficiënt en bovendien dat je precies hetzelfde krijgt als je de regressie van x op y doet, dus het plaatje spiegelt ten opzichte van de lijn y=x. Als ik me niet verrekend heb is er het volgende formuletje die de verhouding tussen lengte hoofdas ellips en lengte korte as van de ellips uitdrukt in r (= correlatiecoëfficiënt) nl.:
verhouding = wortel uit ( (1 + r)/(1 – r) ).
In sommige gevallen is er een negatieve correlatie: dan is de helling van de hoofdas van de ellips -1, dus de richting van de lijn y=-x. Een voorbeeld is waarschijnlijk het verband tussen aantal uren zonneschijn en aantal millimeters regen per etmaal in Nederland. Dat is ook een mooi voorbeeld van de noodzaak van normeren.
In werkelijkheid zijn de puntenwolken geen homogeen gevulde ellipsen, maar in een belangrijk geval wel (bivariate normale verdeling). Dan kun je de wolk opvatten als een opeenstapeling van allemaal volstrekt gelijkvormige grote (weinig) en kleine (veel) wolken, en dan komt er uit al die bewerkingen toch dezelfde regressielijn als bij een zo’n wolk.
Ik heb wat zitten rekenen aan de CITO-scores in de eindresultaten van 2012.
Even een zijspoor: het IQ wordt eigenlijk gedefinieerd als een grootheid die in een bevolking normaal verdeeld is met gemiddelde 100 en standaarddeviatie 15. In principe is het dus eenvoudig om de uitslagen van antwoorden op een batterij vragen om te zetten in een IQ.
Dat gaat als volgt. Je zorgt dat je testpopulatie een getrouwe afspiegeling is van de totale bevolking. Je rangschikt de uitslagen op volgorde. Laten we zeggen dat je testpopulatie 1000 proefpersonen telt. Nummer 500 krijgt dan IQ=100, nummer 841 krijgt IQ 115, nummer 159 krijgt IQ 85, nummer 977 krijgt IQ 130, enzovoorts.
Zo wordt de verdeling automatisch normaal. Zij lijkt natuurlijk al behoorlijk normaal (=klokvormig histogram) omdat het uiteindelijk de som is van een heleboel kleine beetjes (antwoorden op vragen) die allemaal een bepaalde kans hebben om goed of fout beantwoord te worden.
Je kunt dat zelfs doen als de test bestaat uit 100 keer met een dobbelsteen gooien en het puntentotaal registreren. Maar een serieuze test moet zo in elkaar zitten dat als je ‘dezelfde’ test nog eens aan dezelfde personen geeft, je ook ongeveer dezelfde uitslag krijgt. Je zou dan natuurlijk ook een combinatie van lengte, gewicht en hoofdomvang kunnen nemen (uitstekend reproduceerbaar, maar helaas heeft dat weinig te maken met snelheid van begrip). Je moet dus ook op de een of andere manier nagaan of de uitslag wat te maken heeft met het vage idee van snelheid en diepte van begrip, kwaliteit geheugen, accuratesse, algemene kennis enzovoorts. Als je wilt weten hoe goed iemand kan leren ga je na hoeveel die heeft opgepikt van het onderwijs en elders. Als je het heel mooi wilt doen, wacht je tot je weet hoe en of de vragen verband houden met hoe de betrokkenen presteren bij het vervolgonderwijs.
IQ-tests waren oorspronkelijk door Binet ontworpen als objectief middel (in tegenstelling tot de vooroordelen van onderwijzers) om in een vroeg stadium leerachterstanden op te sporen. Aanvankelijk produceerde zo’n test een ‘mentale leeftijd’ en het quotiënt van mentale en echte leeftijd was dan het intelligentiequotiënt. Het lag voor de hand dat wie achterlijk of voorlijk was op de leeftijd van 9 dat ook was op andere leeftijden, vandaar het idee dat het IQ een soort leeftijdsonafhankelijke en bij de geboorte vastgelegde constante was.
Bij de constructie van tests zorgt men dat alles wat aangezien wordt voor mentale vaardigheden (patroonherkenning, rekenvaardigheid, verbale vaardigheid, …) in de test voorkomt en men maakt er een punt van dat de vragen zo in elkaar zitten dat ze met elkaar correleren. Dus een vraag die juist extra slecht wordt gemaakt door proefpersonen die de andere vragen juist heel goed doen, die gaat eruit, evenals vragen waarop het antwoord volslagen toevallig is, vergeleken met de uitslagen van de andere vragen.
Over IQ is een boel geschreven en er zijn zelfs complete wiskundige technieken ontwikkeld (factoranalyse) in pogingen om een touw vast te knopen aan de verwarrende hoeveelheid gegevens, en om erachter te komen hoeveel van de verschillen in IQ tussen de mensen aan verschillen in genen liggen, en hoeveel aan verschillen in ‘omgeving’.
Het is duidelijk dat je zulke tests voortdurend moet herijken. Het is gebleken dat in vele landen in de loop van 1 generatie de tests zover herijkt zijn, dat de populatie in feite een hele standaarddeviatie (=15 IQ punten) is opgeschoven. Niemand weet hoe dat komt. Betere voeding en minder kinderziekte (=> hersenen groeien beter)? Of gewoon beter onderwijs? Of worden de kinderen handiger met het invullen van tests (als je in de laatste minuut alle openstaande meerkeuzevragen random invult, kan je dat punten schelen, ten minste als foute antwoorden geen aftrek geven). Niemand weet het, en voor mij is dat de voornaamste reden om IQ’s als veredeld koffiedik te beschouwen, met hooguit een enigszins voorspellende waarde voor prestaties in het onderwijs, maar niet beter dan bijvoorbeeld een uniform toelatingsexamen.
Bij de CITO-toets zie je dat de meeste scores overeenkomen met een heel smalle band aan ruwe scores. Bijvoorbeeld 540 komt overeen met ruwe scores 156, 157, 158 in 2012, en met 159, 160, 161 in 2011 (je ziet dus dat men elk jaar opnieuw bedenkt wat bijv. ruwe score 159 inhoudt). Bij 550 is het zelfs zo dat dit de hele band van 185-200 omvat.
Laat ik eens veronderstellen dat score 543 betekent 34 fouten in 200 vragen. Zou iemand die 34 fouten maakt in 200 vragen de volgende keer weer exact 34 fouten maken? Laat ik verder even veronderstellen dat de helft van die fouten komt doordat iemand iets gewoon niet weet of verkeerd onthouden heeft, en de andere helft door gebrek aan accuratesse (spelfouten, rekenfouten, opgave verkeerd gelezen enzovoorts). Wat is de kans dat iemand die gemiddeld 17 van 200 vragen door slordigheid fout doet, bij toeval de volgende keer maar 11 slordigheidsfouten maakt? Die kans is 7%. Omgekeerd, als iemand gemiddeld 9 slordigheidsfouten maakt (=CITO 545, vwo advies) wat is dan de kans dat het er bij een andere gelegenheid 12 of meer zijn (geen vwo-advies)? Die is wel 42%!
Ik vermoed overigens dat in de hogere regionen (548 en meer) de meeste (meer dan 50%) fouten slordigheidsfouten zijn. Het kan ook zijn dat slimme kinderen toevallig op scholen zitten waar de leraar zelf niks weet (en misschien niet eens behoorlijk rekenen en spellen kan) en die dus allerlei dingen niet weten die kinderen op betere scholen wel beheersen. Maar die groep heeft het natuurlijk ook moeilijk in het vervolgonderwijs. Overigens zijn slordigheidsfouten gedeeltelijk ook het resultaat van slecht onderwijs, niet van slechte breinwerking. Het vereist een zekere discipline om slordigheid te vermijden, en die moet worden getraind net als zwemmen, voetballen en tienvingerblind typen. Niet iedereen wordt zwemkampioen, maar zwemmen kun je leren, en als je het niet systematisch leert, dan wordt het niks. Een andere bron van slordigheid is natuurlijk dat het veel concentratie vergt om gemaakte fouten te corrigeren. Iedereen die de spel- en tikfouten in eigen werk moet opsporen, zal dat weten.
OK, dit alles gezegd zijnde, hier is mijn omrekentabel van CITO 2012 naar “IQ”.
uitslagen 2012
cito uitslag;
mrs = maximale ruwe score behaald in 2012 in deze groep;
laatste cijfer: fictief Cito IQ (CITOQ) berekend uit cumulatieve percentage.
Tot aan ongeveer score 539 geldt
1 cito-punt = 11/8 CITOQ-punt ,
dus CITOQ = ongeveer CITO – 436 + 1,375 * (CITO-536)
Bron van de cijfers:
http://www.cito.nl/nl/over%20cito/pers/uitslagen_eindtoets_basisonderwijs.aspx
Zie aldaar de pdf Rapport terugblik en resultaten, pagina 5.
515 (mrs 88) – 71
518 (mrs 96) – 75
521 (mrs 105) – 80
524 (mrs 113) – 84
529 (mrs 127) – 90
531 (mrs 133) – 93
533 (mrs 139) – 96
536 (mrs 147) – 100
539 (mrs 155) – 104
542 (mrs 164) – 110
545 (mrs 172) – 116
546 (mrs 175) – 118
547 (mrs 178) – 121
548 (mrs 181) – 125
549 (mrs 184) – 129
@google-517c929316f9334703cc418aa3697e85:disqus ik begrijp de redernatie en uw heldere uitleg wat betreft regressie naar het gemiddelde en is een interessant onderwerp. Echter de vergelijking Cito score-IQ score vind ik niet helemaal correct. Bij deze vergelijking wordt het gemiddelde van 536 (Cito-score) gelijk gesteld aan het gemiddelde van 100 (IQ-score), maar is dit niet wat kort door de bocht? Natuurlijk kan je een IQ score koppelen aan de Cito score, maar is dat niet appels met peren vergelijken? Het voorgaande is te onderzoeken (misschien zij die er wel) door een IQ toets parallel aan de Cito-toets af te nemen. Daarbij vraag ik mij echter of je dit wilt. In mijn optiek schiet het, het doel van de Cito-toets dan voorbij. Bovendien vraag ik mij af: is dit een goede vergelijking? Als ik kijk naar wat de beide toetsen meten: de nadruk bij de Cito-toets ligt met name op kennis (wat ze zouden moeten weten/beheersen in groep 8 o.b.v. de landelijke les methodes). http://nl.wikipedia.org/wiki/Cito_Eindtoets_Basisonderwijs. Bij de IQ-test ligt de nadruk met name op de cognitieve vaardigheden. http://nl.wikipedia.org/wiki/Intelligentiemeting
Dit zijn m.i. twee compleet verschillende concepten en daarom niet met elkaar te vergelijken. Uiteraard is er wel enig verband tussen IQ en de score op de Cito, maar is niet per definitie een 1 op 1 relatie. Of is mijn redernatie helemaal verkeerd, juist vanwege de uniforme verdeling?
Mijn redenatie/gedachtespinsels om het voorgaande te schrijven is het volgende:
Enerzijds moet er een bepaalde objectieve maatstaaf zijn om te bepalen wat het juiste niveau is voor de persoon in kwestie als aanvulling op de subjectieve beoordeling van de docent. Anderzijds vraag ik me af hoe objectief is die maatstaaf. Hierbij zijn termen (in het licht van de Cito-toets) als moment opname, slordigheid en andere al de revue gepasseerd. In toevoeging op het voorgaande ben de mening toebedeeld dat de score van de Cito-toets redelijk gemakkelijk te manipuleren is in tegen stelling tot de score van een IQ test. Met manipuleren bedoel ik het continue herhalen van de stof die op de Cito-toets wordt gevraagd en het oefenen met de format van de toets. Hetzij door een overijverige docent of door ouders die graag willen dat hun kind een bepaald niveau haalt.
Een basis school wordt o.a. beoordeeld op de resultaten van de Cito-score. De Cito-score verloopt volgens een normale verdeling. Dus als we kijken naar een individuele basis school zou deze landelijke normale verdeling hierin terug te vinden zijn. Hier KAN m.i. een probleem ontstaan, namelijk: belangen verstrengeling. Zodra een school slecht presteert qua onderwijs, zal dit terug te vinden zijn in de normale verdeling van de desbetreffende basis school t.o.v. de landelijke normale verdeling. Dan zijn er 3 opties als basis school zijnde: 1)Door de leerlingen beter op de Cito-toets voor te bereiden door te oefenen (hierdoor kan het gemiddelde enigszins worden opgekrikt, korte termijn) 2) Voorzien in beter onderwijs (in meest ruime zin, lange termijn) 3) een combinatie van beide. Uit de praktijk weet ik dat veel basisscholen veelvuldig oefenen op de Cito-toets. Door dit te doen, creëer scholen dan juist niet een vertekend (bias) beeld (het gemiddelde schuift op naar rechts) die ze zelf ook nog eens in stand houden? Je zou haast geneigd zijn om te zeggen dat je (ondanks goed onderwijs) als school wordt gedwongen om hierin mee te gaan. Je wilt als school zijnde niet onder de maat presteren om vervolgens als zwak (dit gebeurt natuurlijk niet zomaar) te worden aangemerkt. De volgende link vond ik hierbij wel interessant:
http://www.jmouders.nl/Themas/School/School/Is-oefenen-voor-de-Citotoets-verstandig.htm
Al met al is het kind uiteindelijk de dupe, omdat deze op een hoger niveau wordt ingeschaald dan anders het geval was, met alle negatieve gevolgen van dien. Het voorgaande verklaart misschien ook enigszins het lage percentage “op koers” van de personen die een 545 Cito-score hebben behaald.
Het voorgaande gaat dan weer niet op in de gevallen die juist te laag zijn ingeschaald volgens de Cito-score.
Quote:Jan Bakker (54), Hoogleraar Intensive Care Erasmus Universiteit Rotterdam: “Ik zou niet meer dan een middelmatige leerling worden op de mavo. (http://www.gelderlander.nl/nieuws/algemeen/binnenland/10413656/Slechte-score-Citotoets-is-geen-ramp.ece )
Al met al weet ik niet zo goed wat ik van de Cito-toets moet vinden, maar vind het een interessant onderwerp. Ik vind het vergelijkbaar met een planning van een groot bouwwerk. Echter kan je bij voorbaat al zeggen dat de planning in de praktijk nooit gerealiseerd wordt volgens de planning, door onvoorziene omstandigheden. Het voorgaande is dan natuurlijk geen reden om dan maar geen planning op te stellen. Idem voor de Cito-toets.
Schiet maar raak op mijn redenatie:-P
Ik heb het net met mijn CAD-programma nagebotst. Klopt ! Althans voor deze ellipse heb ik het kunnen empirisch aantonen (naarmate het progamma nauwkeurig werkt).
Van een wiskundig bewijz zie ik vooralsnog liever af. (-;) Dat laat ik aan de Grieken van de oudheid over.
Met uw uitleg kan je ook goed zien dat de twede test niet ná de erste hoeft worden gemaakt. Het is alleen een kwestie van gevallen uitpikken en spelen met getallen.
“De” Grieken van de oudheid wisten niet zoveel van kegelsneden, hoewel Archimedes en Apollonius er wel veel van wisten. Maar het is niet moeilijker dan het oplossen van een vierkantsvergelijking, of eigenlijk iets makkelijker. Het vinden van de y-waarde voor zo’n midden is algebraïsch gewoon het bepalen van de halve som van de wortels van de vierkantsvergelijking voor y. Voor die som van de wortels is een erg eenvoudig formuletje. De oplossing van een vierkantsvergelijking (leerstof 3 havo en 3 vwo) kun je namelijk schrijven als ‘iets’ plus of min ‘iets anders’. Dan is dat ‘iets’ natuurlijk het gemiddelde.
Nu moet je nog weten dat de algemene formule voor een willekeurige cirkel, ellips, parabool, hyperbool of lijnenpaar luidt:
a * x * x + 2 * b *x * y + c * y * y + d * x + e * y + f = 0 (dat wisten de Grieken niet en de Arabieren ook niet en dingen op zo’n manier noteren is een vondst van Descartes die nog drastisch verbeterd werd door Frans van Schooten).
Gevalletje ‘is het glas half-vol of half-leeg’.
Een kop als 75% van de slimste basisschool leerlingen haalt zonder vertraging het VWO klinkt helemaal niet zo verschrikkelijk.
De zo gehate CITO scores correleren ook heel goed met de verwachte studie resultaten. En dat zo’n score niet een 100% accurate voorspelling kan doen, lijkt me nogal wiedes… Kinderen zitten nog volop in de ontwikkeling, en na 6 jaren basisschool ga je dan extrapoleren naar 6 jaar voortgezet onderwijs. Natuurlijk kun je dat niet met oneindige nauwkeurigheid doen!